��ǮɥN�X�X�ƾǡX�X���i���q���y��X�X���X�X��l�סX�X�q�y�X�X�ƾǮ���
�X�X�q�y����L�ʽ�X�X�����i�ʻ��X�X�q�ϷP���X�X�q�ϤO���X�X�q�ϳ��X�X���P
��q�����X�X����B�ʻ��X�X���O�Ǣw�w���Ф��R�X�X�q�i�X�X�ƾǧ@�ΡX�X���G�z��
��ǮɥN
�p�G�ڭ̦��������z�ѧ�Q�E�@���ݰ��O��ǮɥN���}�l���ܡA����A��]�ä���
�Ȧb��A�ƦܥD�n���b��A�ڭ̹�۵M���{�Ѧb�Q�E�@�������F���t���o�i�C�ۦ��H��
�H�ӡA�H�̴N�b��s�۵M�G��l���ͬ��N�N�O�磌�ʪ����q���Ѫ��B�ΡA����������
�P�J���N�O�ھڷ��ɤw�����ҾڳХߪ��@�ɩM�H���_�����z�סC���b�̪�@�ʦ~�Τ@��
���Q�~���A�H�̹��۵M���t�z������[�����ܤF�A�]���ڭ̻{�Ѩ�H���P��P�@
�ɡA�@�˪A�q�ۦP�����z�w�P�L�{�A����P�@�ɤ��}�ӦҼ{�A���[��B�k�ǡB�tö�P
���窺��Ǥ�k�A�����i���Ω�¬�ǭ�Ӫ��D���A�ӥB�b�H����Q�P��ʪ��U�ؤ��P
���̮t���h���i���ΡC
�b�H�e�ɥN���j�o�����A�ڭ̬ݨ���ڥͬ����ݭn���ʧN�a���o�i�@�B�����N�G
���N�O�����F���M�o�{�ұa�Ӫ��o�����~�A�ݭn�`�b�o�������C���b�Q�E�@���̡A�ڭ�
�N�ݨ����F�l�D�º骺���ѦӶi�檺��Ǭ�s�A�}�l���b��ڪ����λP�o�����e���A��
�B�ҵo�F��ڪ����ΩM�o���C�o���X�{����A�S����Ǭ�s�P�u�~�o�i�}�P�F�s�����C
�Ҧp�A�k�Բġ]Faraday�^���q�Ϲ���P���F�o�q���M��L�q�Ͼ������o���A�o�ǵo��
�S�V��Ǯa���X�s���D�õ�����Ǯa�ѨM�o�ǰ��D���s�O�q�C���J�������q�Ϫi����
�Ǭ�s�A���Q�~��a�ӤF�L�u�q���P�L�u�q�ܡA�o�ǧN�S�����z�Ǯa���X�F�@�Ƿs��
���D�C�ڴ��w�o�{�o�áB�G���H�γ\�h�e�f���O�ѩ�L�ͪ����@�ΥH��A�u�~�B���ĻP
�~��譱�����o�F�����n�����G�C�s�w���]Mendel�^�b���f���D�|�̩Ҷi�檺�ܨ���
�Ǫ�����a�ӤF�t�Ϊ��Ӫ�����H�Τp���M��L�������\�h��}
�~�ءA�åB�P�ϤH�̻{�Ѩ�Y�Ǧ����ʴӪ��Y�ǯS�ʪ���Ǫ���z�C�o�ت��Ѧb��
���H�����֧Q�]�\�|���ͤ��i�p�q���v�T�C�`���A��ǹL�h�O���b�g��N��������
�����Ԥu�@�A��������e���ǻ��ӥB���|�������ɭԡA��ǮɥN�N�i�H���w�g�}�l�F�C
���@���үS�����U�ث�Q���\�h�b�Q�E�@���}�l���ɭԴN�w�s�b�F�A�]�ӭn���X�@
�ө��T�����v�ɭ��O���i��C�ӥB�b�N��Ǫ����ΤW�A�ܤ����b�i�檺���j�u�~��
�R�A�]���w�}�l�F�C�b1769�~�˯S�o��N������z�M�Q�v���ɭԡA�u�~���R���D�n�u��
���@�]�T���w�g��F�i�H���Ϊ����q�C�o�O�@�ӹ�Ϊ��o���A��Ӥ~���ά�Ǫ���z�h
��i���B�o�i���C���O�A�ϱo�@�ɪ��|���p�o�ͭ��R���ܤƪ��t�@�j�o���G�q���q�H�A
�o�O�º��Ǭ�s�����G�F�o�ج�s���}�ݥi�H�l����1786�~���不�]Galvani�^���u
�@�C����L�ӡA���F�K�Q�����q�H�ӵo���X�Ӫ��Ϯg��q�y�p�A���¬�Ǥ]���ܤj��
�n�B�C
���ǤH�ݨӡA��Ǫ�������ΡA�N�������D�n���N�C���o�Ǭ��ʹ�H����Q���v�T
���M�ܤj�A�o�O�����B�w�C�M�n�֪��C�H�������귽����O�A�v���a�B��M���i��
�K�a�X�j�}�ӡA�D�n�O�a�F���ά�ǡA�]���A�b�@��H���̡A���ά�Ǫ����n�����W�L
��¬�ǡC�ƹ�W�A�b�L�̬ݨӡA��Ǫ��ӧQ�@�ӱ��ۤ@�ӡA�䵲�G�A��M�i�i�a�M�w
�C�o�O�ҦV�L�Ī��C�H������۵M����O���X�i���G�S����ҡF�H�̳��@�L�z�Ѧa�{��
�X�j����۵M����O�ҥΪ������z�A���i�H������Ӧt�z�������C
�b�ڭ̭n�ԭz���o�@�ɴ��̡A�D�n���ɦV�A�O��ʤO�Ǫ�����P�ƾǤ�k�v�����s
�쪫�z�Ǫ���L�Ǭ줤�h�A�ӥB�b�i����ΤU�A�����Ψ�ƾǩM�ͪ��ǤW�h�C��Ǫ�
��s�A�ܤ֦b�@�ɴ��̡A�M���DZ��Q���F�a�C�b��ӤQ�E�@���̡A�h�Ƭ�Ǯa�����N��
�a�εL�N�Ѧa�꦳�@�ر`�ѩʪ����ѡA�H����ǩҴ��ܪ�����B�����ʽ�Ψ䶡�����Y�A
�N�O������b�A�ӤH������N�O���c�A�]�\���������F�ұ���μv�T�C�\�h���z
�Ǯa�b�Ҽ{��Ǫ������ɡA�{�Ѩ�o�ǷN���O�K�Q�u�@�����]�A�g���_�Y�檺�ҹ�F
���b����ǻP��ڥͬ����A�H�̫o�S���ɶ��ӱq���Ǫ����ת����h�áC
�b���y�P�ԥ˿��ҳ��w����¦�W�A���z�ǻP�ƾǫإ߰_�@�y���_�o�i�P�M�Ӥ@�P��
�j�H�C�o�Ӧ��N�ϤH�̷Pı�`�����u�w�g�@�ҥöh�a�W���n�F�A���ᤣ�|�A��������H
���s�o�{�F�A�ѤU�Ӫ��u�@���L�O���Ǫ��q�˱o��[��K�A��X�ө��㪺�Żإ[�H
��ɽ}�F�C�ƹ�W�A�o�N�O�Q�E�@�������R�ʵo�i�e�i�H�e�H�̪��H���C
�ƾ�
�b�Q�E�@���̡A�X�{�F�\�h�ƾǪ��s��ءC�䤤�ڭ̥�������ƽסB�νP�s�סA
�T���ǵo�i�����h���g������Ʋz�סA�H�Τ@�몺��ƽסC��X�P���R����k�гy�X�@
�طs���X��ǡA�ӳ\�h�o�˪���k�Q���Ψ쪫�z�ǰ��D�W�h�A�o�i��N�O��Ӥɪ��z
��Ǥj��B�e�i�����ʤO���̤j�����ʤO�C
�ƾǥv���Ӹ`���b���ѽd���A�o�̥u�Q�ͽ磌�z�ǥD�n�����㦳�S�O���n��
���X�ӼƾǤ��䪺�����C
�ť߸��]Fourier�^�b1822�~�X�����Q���Ǿɲz�ת��m�������R�z�סn�@�Ѹ̡A
�ҩ��@���ܼƪ���ơA�L�O�_�s��A���i�H�i�}�������ܼƪ����ƪ������żơF�o��
���G��ӳQ���Ψ�ĪQ�]Poisson�^�Ҵ��X�����R��k�W�h�C�����]Gauss�^�o�i�F�Ԯ�
�Ԥ�M�Դ��Դ�����s���G�A�ç�o�ئ��G���Ψ�q�ǤW�h�C�L�åB�إߤF�q�~�t��
�z�סC
�Ԯ�Ԥ�C�X�B�ʪ��L����{���A�ϰʤO�DZo�췥�j���i�B�A���K�y�]William
Rowan Hamilton�A1805��1865�~�^��h�S��o�Ӥu�@���i�F�@�B�C���K�y�Τ@�Өt�Τ�
���ʶq�P���Хh���ܰʯ�A�õo�{��˧�Ԯ�Ԥ��{����Ƭ��@�դ@���L����{���h
�M�w�B�ʡC�L�ٵo���A�|���ơC
�ĥd�̡]Saccheri�^�b1733�~�A���ڱ��Ҵ���]Lobatchewski�^�b1825�~�M1840�~�A
�����b1831�~�M1846�~�A�i���]Bolyai�^�b1832�~���O��ڴX���o�X��ǩҨ̾ڪ��@��
���w�i��F�Q�סC1854�~�A���ҡ]Riemann�^�P�ϤH�̴��M�`�N��D�ڴX���o�X��ǡA
�H��ͧQ�]Cayley�^�B�����Sþ�̡]Beltrami�^�B�����i�N���]Helmholtz�^�B�J�ܦ]
�]Klein�^�A�h�w�����S���F���֤u�@�C�o�ǧ@�̳����X�A�ڭ̥i�H�b�ƾǤW�Q�D��
�X���o�Ŷ����ʽ�A���o�˪��Ŷ��O�_���P�x�һ{�ѳo�Ӱ��D����˪����סC��R�]
���Z�إߤF�{�N���۹�ʲz�ת��ɭԡA�L�̪���s�~�b���z�ǤW�ܱo�ܭ��n�C
���i���q���y��
�����j�ת������O�q�H�̪��P�x��ı�ӨӪ��A�ūp���U�ڭ̥h���q���C���X�y
�]Amon-tons�^�Q�Τ��ȧ�i�F�������ūp�A�حۮ��S�]Fahrenheit�^�B�C������
�]Reaumur�^�P�Ẹ�����]Celsius�^�U�۽T�ߤF�ЫסC�����Ǽ��ο�g�B��y�M�ǾɤT
�̪��ϧO�A�H�μ��q�������A���O��Ӫ���s���D�C���M�̱ӾU���۵M���Ǯa�A�p���y�B
�i�q�ջP�d��}�����ɦV��{�����O������I��Ÿ�ʡA���b�٨S���P�ڭ̪���q�[����
�����T�w�����H�e�A�L�̪��N���O����o�i���C�n�e�i�@�B�N�ݭn����ݰ��O�@�إi��
�ת��q�A�Ѥ@����Ǩ�t�@����ɡA�ƶq���M�������ܡC�b�o���[�������ɤU�h�i���
��A�N�ݭn������ʽ赹���T�w�ӾA�X�����z�C��O�N���@�ؾǻ����B�Ӱ_�C�o�@�ǻ�
�{�����O�L�����A�J���i���ӤS�L���q���y��A�b���骺���I������ۥѦa�y�q�C
���ܧJ�]Joseph Black�A1728��1799�~�^��M�F����M�ūר�ط����V�c�_�Ӫ���
�k�A���O�٤����������q�P�j�סC�L�q�]�H�s�t�o��ҵo�A��s�F�B�Ĭ����Τ��Ƭ��T
�����A�ܤơC�L�o�{�b�o���ܤƸ̤j�q�����Q�l���A�ӷūo�����ܡC�L���o�Ǽ����F
�u����v�C�L�H�����y��Ρu����v�P�B���X�Ӧ����A�����u��ƦX���v�A����A�P��
�ƦX�Ӧ��T�C�L���q�����A�ĸѤ@�w�q���B�����һݪ����q�P��P�q�����[����ؤ�
140�שһݪ����q�۵��A���u�����Ʀr�O�ؤ�143�סC�L�٧C���F�T�ƪ�����A��967��F
�~��810�סC���o�ش��q�n�Q����T�O�������C���ܧJ�S�ХߤF������z�רӸ�������
��Ϥ��P����o�ͬۦP���ū��ܤƩһݪ����q�O���P���A��ӥL���ǥͥ캸��]Irvine�^
�ԲӦa���w�F�@�Ǫ��誺����C�o�˥L�N�ХߤF���q���w����k�A�Y�q���N�C���軡��
�����y�黡�@���ɬ�ǫe�i�A��1840��1850�~���A�����i�N���P�J�դ~�ҩ����ʵ����A
�T�ߤF���O�B�ʪ��@�ؤ覡���[���C
�t�@�������y�黡�A�Ϊ̻��Ĺ諸��y�黡�A�ɤF�q���{�H����s�̫e�i�C�n��
���ѩ����ӱa�q����Ӫ��鬰�����ۤީάۥ��A�i�H���w�q�O�P���ۦ����@�ت�
��A�O�@�إi�[��q�C���b�q���������v���A�ڭ̲M���a�{�Ѩ즳��ؤ��P�ӥB�ۤ�
���q�C�����P�������ҥͪ��q�A�i�Q�w�P��ּ����ҥͪ��q���M�C���F�����o�ǵ�
�G�A�y�黡���]����ةʽ�ۤϪ��y��Ϊ̦��@�جy��A���b��`�q�h�Τ֮ɡA�N�ް_
�a�q�����A�C�ڭ̲{�b�٦b�ϥΥ��q�B�t�q���A�X���y�軡���\�h�N�y�A���M�ڭ̤w
�g���D�q���O�s�y��ӬO�L�ɪ����c�A�o�O�ڭ̦b�᭱�n�������C���H�̥ΰ_�q��
���ͥX����j�q���q�A�A�J�W�b�ӹy�~�]�@�Ӥ��~���K�W���䪺�����~�^�@���q�e����
���ɭԡA�N������a�ӫܤj��K�C��p�]Stephen Gray�A1729�~�^�B���O��]du Fay�A
1733�~�^�P���Q���S�C�]Priestley�A1767�~�^�������M�F�ɹq��P���t��A�o��N�y
�h�O�w��j�Q�J�]Desaguliers�A1740�~�^�ҩw�X���C
�H�̤@�`�N��q�~��q������P�n�T�A�]�N���W�{�Ѩ쥦�̻P�p�q�ۦ��A�]�Ӥ]�N
�ä߳o��ز{�H�ʽ�@�ˡC��ˤ~���ҩ����ʽ�ۦP�O�H��ˤ~��ϤѤW���p���A�q
���z�ǩw�ߩO�H�I���J��]Benjamin Franklin�A1706��1790�~�^��o�Ӱ��D���G�J�F
�g�C�L�d�U���\�h�H���̳��yø�F���֨ӹy�~��q������A�ô���ѹq�����ƪ��ݡB��
�}���赥�����C
�b�a�q��y�ݪ���q�@�Ϊ��ҵo�U�A�F�Q�ڼw�]d�zAlibard�^�P��L�k��H���ͤF
��{�q�ǾɤU�Ӫ����Y�C1752�~�A�L�̦b���̦a��˸m�F�@�ڰ�40�`���K��A�n�u�M�w
�a���{�q�����O�_�a�q�����D�v�C���q���b��W�g�L�ɡA��U�ݧY�o�ͤ���C�o�ӹ���
�b��L��a�]���ư��L�A�ӥB�������\�X�X�ƹ�W�A�t���o�����̰ҡ]Riehmann�^�б�
���]���b�ΤW�˸m�K��ɹp�q�ӷ����Q���šI�P�ɴI���J�L�h�έ���w���a�i��F�P
�˪�����C
�b����D�쪺���ݸˤW�@�ګܦy���K���A���媺��[���X�@�`�E�C�b��÷���U
�ݻP�Ⱶ�Bô�W�@�ڵ��a�A���a�P��÷�s�����B�i�t�@���_�͡C���p�B�n�Ӫ��ɭԡA
�⭷���X�A��÷���H�������b���ε����A�Φb����B���U�A�K�ϵ��a����F�P�ɶ��`
�N������÷�I����ε�����l�C�p���@�g�L���媺�W�šA�y���K���N�i�q�p���l�q���A
�ϭ���M��ڳ�÷�a�q�A��÷�t�@�ݪ��ֺ����V�|�P�i�}�A�Y�N�������A�N�|�Q��l
�ޡC������P��÷���Q�B��A�ӯ�ۥѶǾɹq���ɡA�A�Y�N�������A�K�|�ݨ��j�q��
�q���_�ͬy�X�C�q�o���_�ͨ��̥i�H���p�~�W�q�F�Ѧ��o�Ӫ��q���i�ϰs��U�N�A�å�
�Ӷi��O�������q������F�ӳo�ǹ��祭�`�O�a�����p�y�Τp�ިӰ����A�o�˴N������
���o�عq������M�ѪŪ��{�q�O�P�˪��C
�Q�K�@���ɡA�H�̶i��F�\�h���[����q��۵��q�ۻP����ӥq������A�ӥB�q
���@���q���൹�H�H�·��ʥ������{�H�A�]�A�פް_�H�̪��`�N�C���H�ҹ�F���̪��q
���x�A�˲M���̵����H���������T�O�ѩ�q���{�H�ҭP�C
�q�O�M�ϤO����s�}�l��Q�K�@�����~�C�̷����M�k��x�Ƥu�{�v�w�ڡ]Coulomb�^
����b1750�~���k�M1784�~�o���A�ҿקᯯ�A�Y�@�����������K���A�b���I�Wô�W�@��
���K���A���b�@�Ӭ����X���C�w�ڧ�@�ӱa�q���y��b�K�����@�ݡA�A���@�ӱa�q���y
�P������A�o�K���Y�|����C�L�S���@�����K�����K���A�A�Υt�@���K�M������]�i��
���K���@������C�L�γo�Ӥ�k�o�{�q�O�M�ϤO���H�۶Z�����誺�W�[�Ӵ�֡A�ҩ��o
�ǤO�q�M���y�ҩ����ޤO���P�˪����Y�C�L�ٵo�{�q�O�P�q���q������A�]�ӥi�H�ιq
�O�Ӷq�q���C�o�Ӧ����q�O���w���٥���Ѵ��Q���S�C�M�d��}���Υt�~����k�o�{
�L�C�L�̥ι����ҩ�����Ϊ������X�a�q����̭����S���q�O�A�ҥH�y�餺�]�S���q�C
���y�L�h�μƾǤ�k�ҩ��A�p�G����Ϥw�ߦ��ġA�@�ӥѨ㦳�ޤO������c������
�òy�߹��䤺�����@�Ӫ���S���O���@�ΡA�ӥB����O���O���w�߳����|���o�ӵ��G�F
�P�˪���s�]�A�Ω�q�O�C
�O���w�߬J�M���ߡA�ƾǮa�N���R�q�Ǫ����D���L�h�A�ɥX�@�t�C�P�K�����Y�A�b
�i�H�P�[��G��������p�U�A���ҩ��P�[��G�����ŦX�C��������q�������G�A��
����q�O�P�q��A����P���t�骺�U�رƦC���q�e�q���A�b�����B�ĪQ�P��L����
�����⤤�A���ҩ��i�H�μƾǤ�k�B�z�C
�q�O�@�صL���q�B���i���Y���y�骺�ǻ��M�q�O�@�ӽT�w���q���[���O�@�P���A��
�M�b��s�W�ä��O�����i�֪��A�ƹ�W�o���X�@�ӫK���M��s�o�Dz{�H����K���e
���C
���v�N�q���O�H�̪��`�N��V�q�O�C�P�ޤO�ۦP�A�q���G�]�V�L�Ŷ��ӧ@�Ω�
���B�C�ƾǮa�ݨӳo���ݭn�i�@�B�������A�����z�Ǯa�ܧִN�}�l�����o�ӪŶ����ʽ�C
�]���o�ӪŶ����M��Ǽ���ت����W���P���O�C�ڭ̥H��|���D�A�o�N�ް_�F�{���s��
�u�����z�ǡv���{�N�z�סC
���
���q�P�q����c�h�A�H�̹L�h�N�P��Q������K�A�ܤ����M�p���C�k��H������
�ߤF�X�誺�B��K���Q�i��ӥN���o���c�h�����C1791�~�A�k����ij�|�����F�@
���M���e���|�����i�A1799�~�����F���ݪ��q�зǡA�èM�w���ΡF1812�~�M�w�ۥѨ�
�ΡA1820�~�j���I��C
���ת����O�̡A��өw���q�L�ھ����a�y�g��@�H�����@�d�U�����@�C����
�ڤW�A�@�̪����O�������s�ɬY�@�����ݴΨ��I�����Z���C��Ӥj�a���q����T��
�W���A���D�̪��ä���n����a�y���g�骺�@�ӶH�����Y�z����A�����[�H�勵�C�e�q
�����O�߯S�ΤɡA�����O�C��@���̡]1/10�̡^���ߤ���A���H�䤣���q�סA1901�~
�W�w���@����]�d�J�^���¤��b�@�j���������|�ס]�b�o�ūפU�����K�׳̤j�^�U��
�e�n�C
��q�����O�d�J�Τ���A��ӳW�w���C��@���̪��¤��b���|�פU����q�A��
�{�b�h����1799�~�ǶO��-���ա]Lefebre��Ginneau�^�P�k�������]Fabbroni�^�Ҩ�w
���`�v�X���зǿž�����q�C�L�̪��u�@����T�ץi�q�N���i�]Guillaume�^�b1927�~
�ҩw���̷s�߯S�ȥh�P�_�A�Y�@�߯S���ȵ���1000�D028�ߤ����̡C
�ɶ������O��A�w�������Ӷ��骺1��86400�A�ҿץ����Ӷ���O��Ӷ����߲Ĥ@
���L�l�Ƚu�M���s�ĤG���L�l�Ƚu�������ɶ��@���@�~�p��X�Ӫ������ɶ��C
1822�~�A�ť߸��b�L���m�����z�סn�̫��X�ƶq�ξɨӶq���q�Ӫ��ܮɡA���Y
�ǬO���C���]�HL�����סAM����q�AT���ɶ��A�h�t��u�]�Y�b���ɶ����Ҹg�L�����ס^
���q����L/T��LT��1�C�[�t�O���ɶ����t�ת��ܤơA��q����v/T�A�YL��T2��LT��
2�C�O�O��q�P�[�t�ת����n�A��MLT��2�F�\�OML2T-2�C�����ѳo�ǰʤO���ɥX�q�P
�Ϫ����A�H���٭n����C
���b1870�~�A�F���@����ڨ�ij�A�@�P�P�N���Τ@����Ǫ��q�רt�ΡA�H���̡]1
��100�̡^�B�J�]1��1000����^�M���T�̧@�����A�o�N�O�`�������̡B�J�B��
�]C�DG�DS�^��C
��l��
�e�X�����A�ڭ̤w�N�w�ӧJ�Q�S�ɥN�H�Ӫ���l���DZԭz�L�F�C�o�ӭ��Ǹg�Ȩ���
�h�w�饸��A�b���@������A�A��������_���H��A�~���s���D�_�ӡC���Q����
�P�o�ӭ��ǡA����f�Υ�����|�P�c�J�ܭת��y�����s�[�H�ԭz�F�i�q�ջP���y�b�L��
����ƾǻP���z�Ǫ���먣�Ѥ��]�ΤF���C�q���ɥH�ᥦ�S�Q���m�A���M�����M���z�b
��ǫ�Q���C
��F�Q�E�@����~�A���Q�H���s���X�A�H�����T�B�G�B�𪫽�T�A�����z�ʽ�A�H
�Τƾ��ܤƤW���w�q�ƹ�C
��½�U�����H��A�H�̹磌�誺�T�A�ΤT�ۦ��F��M�����{�ѡC�������M���T�A�A
�ڭ̳q�`�{�ѳ̲M�����`�O�䤤�@�A�A�p�ڭ̻{�ѳ̲M�������g�`�O�G��F�����i�ܬ�
�T�A��������@�A�A�p�N���h���B�A�]�o�h���T�C�H�۳o�ػ{�Ѫ��i�B�A�H�̶}�l��s
�ƾǤƦX�w�ߡC���骺�ƦX�w�ߡA�̮e���o�{�A�]���A����N���A�O�@�د������B�b�F
�����A�ӻP��L����o�����Y�F�C
�ھں�K���R�����G�A�H�̡A�ר�O�ԥ˿��B���|���S�]Proust�^�P���ƯS
�]Richter�^���o�{�@�ӤƦX���l���@���t�a�ѦP�q�������Ҳզ��]�b���ɹF�쪺��
�פU�^�A�o�өw�q�ƦX���[���A�b�s�ƾǪ���t���_�F���n�@�ΡA���M���M��������
�]Berthollet�^�������q�����ѬO���ۦX���C�����O��˱o�Ӫ��A�`�O�B�P���1�P8
����ҦӦX�����C�]���ڭ̱o��ƦX�����[���A�p�H�B���ƦX����1�A�h�ƦX����8�C
��ؤ����H�h�ؤ覡�ƦX���h�ؤƦX���ɡA�@�ƦX������ئ�������һP�t�@�ƦX����
��ئ�������ҡA�`��²�檺���Y�G�b�@�ƦX����14����P8����ƦX�A�b�t�@�ƦX��
���h�P16����ƦX�A�ꬰ�e�̪��⭿�C�i�O�b�P����o�{��A�o�ةw�q�ƦX�������y��
���ܡA�H���٭n�ͨ�C
�����E�D���y�]J.Dalton�A1766-1844�~�^�O�´��S�����]West morland�^�@�Ӥ�
��´�u����l�A�b�L���p�DZЭ����}�ֶ��v�̡A�DZo�@�ǼƾǻP���z�Ǫ����ѡC�L�b��
�����S�o�ۤ@�ӱЮѪ���m�A�}�l�L����骺����C�L�ݨ���骺�ʽ�̦n�έ�l�ץh
�����A��ӥL��o���[�����Ψ�ƾǤW�h�A���X�i�H��ƦX���{�H�������㦳�T�w���q
���۲����I�����X�A�ӨC�@���������I������S�w�����q�C�L���G
���馳�T�ؤ��P���Ϥ��ΤT�A�A�S�O�ް_���Ǫ��ƾǮa���`�N�A�Y�u�ʬy��B�G��
�P�T��T���ҥN�������A�F�ڭ̩Ҽ��x���ܦ��W���Ҥl�O���A���b�Y�DZ��p�U�A�i�H��
���T�ت��A�C�b�]�T�A�ڭ̬ݨ����O�����u�ʪ��y��A�b���A�O�������G��A�b�B�A�O
�������T��C�o���[��G�q�q�a�ި�@�Ӧ��G�o�줽�{�����סG�Z���۷��j�p������A
���ޥ��O�G�馡�T��A���O�ѵL�Ʒ��L�p�����I�έ�l�Ҳզ��A�L�̬��@�ؤޤO�ҧ����A
�o�ؤޤO�]���p���P�Ӧ��j�z���t���C�K�K
�ƾǪ����ѻP�X�����L�O��o�ǽ��I���}���p�X�C���誺�s�Щη����O���b�ƾǧ@
�Ϊ���O�d�����C�ڭ̭n�Q�гy�η����@�ӲB�����I�A�M�b�Ӷ��t�̼W�[�@���s���B
�η����@���T������P�A�@�˪����i��C�ڭ̩үవ�쪺���ܡA�u�O���ߵ۪��A�U�Τ�
�X���A�U�����I���}�A�H�Χ��Ӥ��������I�p�X�_�ӦӤw�C
�b�@���ƾǬ�s�̡A�H�̳����T�a�{���A�˲M�ƦX����²�榨�����۹ﭫ�q�A�O�@
�ӭ��n���ؼСC���L�A�������O�A�L�h�ƾǪ���s�N����b�o�̡F�H�̥��ӫܥi�H�q��
�誺�۹ﭫ�q�A���X���骺�����I�έ�l���۹ﭫ�q�A�Ѧ��ݥX�A���̦b�U�ب�L��
�X�������ƥػP���q�A�Ψ����U�M���ɧڭ̥��Ӫ���s�M�勵��s�����G�C�]���A����
���@�ӭ��j�ؼСA�N�O�������w�U�C�X�Ӷq�����n�ʩM�n�B�G����P�ƦX���������I
���۹ﭫ�q�A�զ��@�ӽ������I��²����I���ƥءA�ѻP�c���@�Ӹ��������I����
�������������I���ƥءC
�p�G��A�PB��ӥi�H�ƦX������A�H�U���q��²���ƦX�}�l���U�ؤƦX���i�স�ǡA
���G
A��1��l��B��1��l��C��1��l�A�G�����C
A��1��l��B��2��l��D��1��l�A�T�����C
A��2��l��B��1��l��E��1��l�A�T�����C
A��1��l��B��3��l��F��1��l�A�|�����C
A��3��l��B��1��l��G��1��l�A�|�����C
�ڭ̥i�H�����H�U���q�h�A�@���@������ƾǤƦX����s�����w�G
1�D�p�G�⪫��ƦX�ɥu�o�X�@�ؤƦX���A�ڭ̥������w�o�ؤƦX�O�G�����A���D
���Y�سy���ۤϱ��p����]�X�{�C
2�D�p�G�o�{����ؤƦX���A�h�������w���̤@�ӬO�G�����A�@�ӬO�T�����C
3�D�p�G���T�ؤƦX���A�h�i�w�Ƥ@�ӬO�G�����A��L��ӬO�T�����K�K�����C
��o�dzW�h���Ψ�w�g�d�����ƾǨƹ�W�h�A�ڭ̱o��H�U�����סG1�D���O�B�P
�G���ƦX���A�o��ؤ�������l���۹ﭫ�q����1�G7�F2�D��O�B�P�᪺�u���ƦX
���A�o��ؤ�������l���۹ﭫ�q����1�G5�F3�D��ƴ᪺����O��P�G���ƦX���A
���̪���l���q��5�P7�F4�D��ƺҬO�Ѥ@�Ӻҭ�l�P�@�Ӯ��l�c�����G���ƦX���A
�@������12�F�һĮ�O�T���ƦX���]���ɤ]�O�G�����^�A�����@�Ӻҭ�l�M��Ӯ��l�A
�@����19�F�����C�H�W�U�ر��ΡA���O�H�B��������l�����Ӫ��F��L���������q�C
�D���y���ԭz�A�۵M�]�t�۷������K�����~�G�Ҧp�L�N���ݰ��O�@�طL�����y��F
�L���ƦX���q�]����T�A�p�H�B�����ɡA���q���ӬO8�A�ӥL�w��7�C�L���w�A�p
��ؤ������ƦX���u���@�ءA�K���ݰ��O�@�ӭ�l�P�t�@�ӭ�l�����X�C�o�ذ��w�]��
�O���M�A�Ϊ��A�]���A�L�����M���c�~�����~���[���C���M�o�ˡA�D���y��ҽk
�������ܦ��F�T�w����Dzz�סA���T���o��ǥv�W�����j�i�B���@�C
�D���y�b�p��餤�[�W�I�B�P�M�Q�r���O���ӥN����������l�C�o�Ӥ�k��Ӭ���
��ƾǮa�f���d���]Berzelius�A1779��1848�~�^�[�H��i�A�Φ��ڭ̲{���ҥΪ���t�A
�Y�Φr�����Ÿ��h�N���P�@�Ӥ�������l�q�۷����Ӥ������۹��q�C�ҦpH���O�ҽk
�a�N���B�����A�ӬO�N������1�]1�J�B1�S�Ψ�L���^���B����q�FO�N������P�@��
�쪺16����������q�C
�f���d�����D�n����u�@�A�O�b���ɥi��d�A�γ̤j����T�רӴ��w��l�q�A
�Ϊ̻��������ƦX�ҡC�L�]�o�{�F�X�ӷs�����A��s�L�\�h�ƦX���A��b�q���Ǫ���s
�W�A���}�F�@�ӷs���g���C�L�P�����]Davy�^�p�X�T�ߤF�q�ƾǪ��w�ߡA�åB�ݨ�
�q���ʻP�ƾǧE�X�O�������K�����Y�C�L��o�[�����s�o�ӻ��A�Ӭ����ɩ����F�ѡG�L
�{���@����l���t�����q�γ��q�ѩ��۹�O�q�A���̤~�ƦX�C�L�{���C�@�ƦX�����O
�a���ʹq���ⳡ���Ҳզ��C�p�G�X�ӤƦX�����ۤƦX�A�ڭ̥i�H�]�Q���O�ѩ�h�l����
�ʹq�����@�ΡC�o�ӤG���ת��z�פ������I��q�W�i�����ѡA�즳���ƾǿ����ɡA�N��
���ҥN���F�C�{�b�ڭ̩��դƾǩM�q��ز{�H���K�������Y�A���L���p�f���d����
�Q��������²��C
���H�̹����ƦX�{�H�[�H��s�x����s�ɡA�D���y��Ӫ���l�[���A�K���{�X��
�ʳ��C�\��Чf�ħJ�]Gay��Lussac�A1778��1850�~�^��������ƦX�ɡA��e�n�`���@
�w��²���ҡA������wù�B��]1776��1856�~�^�b1813�~���X�G�ھڹD���y���z�סA
�M�\��Чf�ħJ���[���A�ڭ̥i�H���_�@���P�e�n������ҧt����l�ơA���w������²
�檺��ҡC�w����1814�~�W�߱o��ۦP�����סA���Q�H�ѰO�Ω����F�A��1858�~�A����
�dù�]Cannizzaro�^�~�A��M�F�o�Ӱ��D�C�쨺�ɡA�H�̤~�q����ƦX���ƹ�H�αq
���z�Ǫ��Ҽ{�ݥX�A�����n��ƾǤW����l�M���z�ǤW�����l�ϧO�}�ӡC�ƾǤW����l
�O����ѥ[�ƦX���̤p�����F���z�ǤW�����l�A�O��ۥѦs�b���̤p���I�C���F�����
�wù���]����²���k�A�O���w�P�e�n������t���P�ƪ����l�C�H��ڭ��٭n�����o��
�G�i�μƾǤ�k�q���z�ǤW���@�Ӳz�ױ��ɥX�ӡA�o�Ӳz�װ��w���骺���O�O�ѩ�
���l�`�b���_�a�B�ʩM�I���Ӳ��ͪ��C
���^��������D�ӡA�G�e�n�]�Y�G���l�^���B�P�@�e�n����ƦX�A�ӱo�G�e�n�]��
�G���l�^�����T�C�����o�����Y��²�檺�z�סA�O���w���z�ǤW���B���l�P����l�A�C
�@���l���t��Ӥƾǭ�l�A�Ӥ��T���l�㦳�i�H��H2O�N�����ƾǵ��c�A�]�ӳo�ܤƥi
�H�U�C��{���h���ܡG
2H2��O2��2H2O
�]2�e�n�^�]1�e�n�^�]2�e�n�^
�o�ˡA�J�M�ƦX�q�O8�A�Ӥ@�Ӯ��l�i�H�M��ӲB��l�ƦX�A�p�G���B����
�l�q�����A�h��l�q���O16�ӫD8�C�ҥH�b�M�w�U��������l�q�H�e�A�ڭ̥���
�N�D���y���ƦX�q�[�H�վ�A�Ϥ��X���ӹ���ҵo�{���ƹ�C�������өҦ��Ҿڨt��
�a�i��F�o�f�u�@���N�O�����dù�C
�ѩ�@�Ӯ��l�M��ӲB��l�ƦX�A�ڭ̴N����l���O2�C��l�����[���A�O
�H��\�h�~���j�����ƾǫ�Q����¦�C
�w���������w�g�ѹD���y�һ{�Ѫ��G�Q�ӼW�[��{�b���E�Q�h�ӡC�����o�{���u�@�A
�O�]�������w���i�檺�C���@�ӷs����s��k���Ψ�ƾǰ��D���ɭԡA�N�`�`�|�o�{�@
��s�����C�q�y�����ѤO��������h�]1778��1829�~�^�b1807�~�����X�P���ݪ��[�P�ǡC
�y����Ф��R�ϧڭ̵o�{䧡B䣡BB�S������C��g�ʪ���k�ϧڭ̵o�{�F�J�M���P
�ڤ@�������A�����y�����л��S�ϧڭ̵o�{�F�\�h�P�쪺�����C
1815�~�A���үS�]Prout�^�N�w�g�b��s��������l�q�P�䪫�z�ʽ褧�������Y�A
�H��������]Newlands�^�P�w�E�v�w�g�ˡ]deChaucourtois�^�]��s�F�o�Ӱ��D�C1869
�~�A�ڭC���]Lothar Meyer�^�P�X��ƾǮa���o�C�C�ҡ]Mendeleeff�A1834��1907�~�^
���\�a�ҹ�F�o�����Y�C���o�C�C�ҧ⤸�������l�q�����ǡA�ѻ��쭫�Ʀ��@�Ӫ��ɡA
�o�{���̦��@�ضg���ʡX�X�H�������ҫ��X�L�����ˡA�C�ĤK�Ӥ��������@�ǬۦP����
��A�@�������i�H�ӳo�˱Ʀ��@���A�ϦP�ʽ誺�����k��@��̥h�C�Q�γo�˻s�����P
�����A�i�H�⥿�T����l�q���P��l�����w�������A�������ťեѪ��o�C�C�Үھڰ��]
�[�H��ɡA�o�˥L�N�w���F�@�ǥ����������s�b�Ψ�ʽ�A�䤤�@�ǫ�ӳ��Q�H�o�{�F�C
���o�C�C�һ{���L���g�����u�O�º�g��ƹꪺ�ԭz�C���o�˪����Y�o�U�i�קK�a
�ϤH�^�쪫�観�@�P��¦�����[���W�h�C�\�h�H�H���o�Ӧ@�P��¦�i��N�O�B�A�L�̷Q
�ҩ��p�H�B����l�q�����A��L��������l�q�����O��ơC���M�\�h��������l�q��
���ơA�����X�Ӥ����A�Ҧp��]CI��35�D45�^�x�T�a�����q�o�Ӥ�סA���]Stas�^
���H�W�[���w��l�q����T�ץH��A�]��������o�Ӱ��t�C�n�ҩ�����㦳�@�P��¦��
���l�q�k������ơA�ٱo���ԥb�ӥ@���F�o�ؤu�@�O���ɪ�����M�z�ׯ�O�줣�쪺�C
�q�y
�ڭ̦b�W���ԭz���U���������_�q�����A���D�n�O�Ψӧ��R�q���ᤩ�Y�ص��t�骺�C
���T�A�p�G�ϰ_�q�����a�A�Φ��@�Ӿɹq�q���A�h�b�o�q�����N���@�I�q�y�q�L�C���L�A
�N�O�b���u�}�������_�q�����A�C�@�����q�L���q�q�]���D�`���֡A�H�P�n�Q�b�o�q��
�W�o�{�q�y�A���O�ܧx�����A���M�A�p�G�b�ɽu���d�@�ӪŮءA�h�o�_�q���ҥͪ�
���q��t�A�i�H���ͥi��������C
�Q�E�@����A���不�Υ�S�q�����o���A�}�P�F�@�ӷs����s���C�o�عq���ް_
�F�@�t�C�{�H�A�̪�A�٬����不�y�A�g�L�\�h�H���V�O�A�C�C�a�M�t�~�@�t�C�H�q�o
�W���{�H�pô�_�ӡC�ڭ̲ש���թҿצ��不�y�A���O�q���y�ʡA�u�O�M�_�q���ҥͪ�
�q�q��_�ӡA�j�ܦh�A����q��t�o��q���ҥͪ��q��t�p�o���p��ơC�ѩ�b�q����
����@�I�W������o�{�n�s���q�A�ڭ̤]������q�y�@�ؤ��i���Y���y��b���i��
������ʺޤ����y�ʡC
��S�q���O�ѩM���[��ӵo�{���C�o�ӵo�{�A�̪���G�n�ި�t�~�@�Ӥ�V�h�C
1786�~���k�A�N�j�Q�H���不�o�{��L�b�_�q������q���v�T�U�o�ͦ��Y�C�b�o���[��
����A�L�S�o�{�G�p�G�ϯ��g�M�٦צP��ؤ������������ݳs���_�ӡA�ӨϪ��ݤ��۱�
IJ�A�]�i�H�o��P�˪����Y�C���不��o�ǮĪG�k�]��ҿסu�ʪ��q�v�F��ӡA�t�~�@
�ӷN�j�Q�H�����Ȫ���S�]Voita of Pavia�^�X�ӡA�ҩ��o�ذ{�H�ä��̿��@��
�ʪ����誺�s�b�C1800�~�A��S�o���A�H�L���m�o�W���q���C�b�Q�E�@����~�A�o�عq
�������@�ج�s���u��A�b��S�M�L���P�ɥN���O��H�⤤�A���ͤF�@�ǫܦ��������
�G�C���ɪ�������x�n���F�_�����s�o�{�������C���ɪ��H���η��j�������h��s�o��
�o�{�A����P���{�סA���ȩ�@�@���H��A�H���������餤����q�P��g�{�H�ɡA�Ҫ�
�{�X�����ؼ��աC
��S�Ҩ�q���A�O�Τ@��N�L�B�ɽL�H�ά������Q�����㪺�ȱi�A���U�C���Ǭ�
�|�Ӧ����G�N�A�ɡA�ȡA�N�A�p�������K�K�̫�O�@�ӻɽL�C�o�ˤ@�زզX�A���N�O
�@�ӭ�l����q���աC�C�@��p�L�����㪺�ȹj�}�A�Ӧ��@�ӹq���A�y���ֳ\�q��t�C
�o�Ǥp�q�����q��t�[�b�@�_�A�K���F�q���ջɾN��ݪ��۷��j���`�q��t�]�Τ����
�a�s���q�ʤO�^�C�t�@�ظ˸m�k�O��Y�z�˦��Q���ε}�Ī��M�l���X�b�@�_�A�C�ӪM�l
�˸m�@���N���M�@���ɤ��C�e�@�M�l���N���P���@�M�l���ɤ����p�A�o�ˤ@���~��U�h�A
�d�U�̥��@�ӾN���M�̫�@�ӻɤ��A�@���q���ժ��ⷥ�C��S�H���ĪG���ӷ��b���ݪ�
�p���B�F�]����L�M�ⷥ�����ݤ������Ǥ~�p�H�W�ҭz�C�o�Ǫ��ݤ��ζ�L���[�K�o�{
�O�L�Ϊ��A���M���̦b�o�ػ����������ϵe���������n�a��C
�p�G�ڭ̱q��S���q�����ιq�y�A��j�K���t�a�I��A�D�n�ѩ�ɤ��������W��
�F�@�h�B�C�o�عq���ơA�i�β��Ļɷ��G��¶�ɤ��Ӫ���A�o�˥ͦ�������O�ɦ�
�D�B�F�ΥκҴΥN���ɤ��A�⥦��b��ƾ��p�v�ĩέ��]�Ĺ[�����G���A�o�˩Ҳ��ͪ�
�B��N�ߨ��ܬ����C
�ƾǮ���
����S���o�{�������b1800�~�Ǩ�^��ɡA�ߨ�N���H�i��s�@�ǰ��[��A�P��
�F�q�ƾǪ��ϥ͡C���캸�ˡ]Nicholson�^�P�d�ܺ��]Carlisle�^�b���S�q�������
�˸m�[�H���ܮɵo�{�G�p�G�Ψ�����ɵ��s���q�����ⷥ�A�A�N��u���L�ݮ��b�����A
�èϨ䤬�۱���A�@�ݦ��B��o�͡A�t�@�ݪ����ɽu�Q��ơC�p�Υժ����ζ������ӥN
�����ɵ��A�h���o�ͮ�ơA��H���骬�A�X�{�C�L�̪`�N��B�𪺮e�n������𪺤G���A
�o���O�B��G��ƦX��������ҡC�L�̻����o�ز{�H�N�O�������ѡC�L���٪`�N��ϥ�
��Ӫ��˸m�ɡA�q�����]���������ƾǤ����C
���[�A�J�|�J���J�]Cruichshank�^���ѤF�����B�һĶu�]Ĭ���^�M��]������
�ȡ^���G�A�åB�q�ȩM�ɪ����G���A�N�o�Ǫ��ݨI���X�ӡC�o�@���G�H��ɭP�q�᪺��
�k�C�L�S�o�{�b�����P�G���ܦ��P�ʡA�ӳ����P�G���ܦ��ĩʡC
1806�~�A������h�]1778-1829�~�^�ҩ��ĻP�P���Φ��O�ѩ���������誺�t�G�C
�L�b�H�e�w�g�ҩ��A�Y�ϱN�q����b��ӪL���A�������Ѥ]�i�i��A�����δӪ��ΰʪ�
���ƱN��ӪM�l�p���_�ӡC�P�ɥL���ҩ��q�����P�q�����ƾ��ܤƦ��K�����Y�C
��S�{�����不�{�H�P�q�O�P�@�{�H�C�o�Ӱ��D���F�\�h�H��s���D�ءC��1801�~�A
�U�Դ��y�]Wollaston�^�ҩ���̵o�ͬۦP���ĪG����A�~�T�w��̽T�O�P�@�{�H�C
1802�~�A�J���ҡ]Erman�^�ϥ���q�����q�F��S�q���Ҵ��Ѫ��q��t�C�o�ɡA�~����
�Ѳ{�H���{�u��i�����q�v�A�ӷs�{�H���{�u�B�ʤ����q�v�C
���Ӥ��{���D�ҡA�ڭ̤@�P�P�N���w�q�V�ҿץ��q��V�y�ʡA�Y�b�q�����ѾN���y
��ɪ��]�κҴΡ^�A�b�q���~�u�۾ɽu�ѻɬy��N�C�ھڳo�ӺD�ҡA�ɪ��٬��q������
�q�A�ӾN���٬��t���C
1804�~�ƨ��溸�]Nisinger�^�P�f���d���ŧG�����Q���G�i�ιq�y���ѡA�İ�X�{
��@���A���ݥX�{��t�@���A�]�ӥL���_�w�G�s�ͩʪ��B�����ä����H�e�Ұ��Q�����ˡA
�O���ݱq���G����������]�C�b���ɩҪ��D�����ݤ��A���\�h���γo�Ӥ�k��ƥX�ӤF�A
1807�~�A��������ѤF���ɻ{���O�������һĹ[�P�һĶu�C�L���j�q�y�q�L�t�����o��
�ت���A�Ӥ����X��H���[�P�Ǫ��ݡC�����O�d�U�����]Cornwall�^�H�A�o���B��z��
�S�|���ܡA�L���F���ɷs���߬Ӯa�ǰ|���ƾ����v�A�L�����t����״I�A�l�ޤF�\�h�H
�h�ѥ[�C
�ƾǤƦX���i�H�ιq����k�Ӥ��ѡA�����ƾǤO�P�q�O�����O���pô���C�����u��
�X�@�Ӱ��]�A���ƾǪ��l�O�P�q���l�O�P�ͩ�@�]�A�e�̧@�Φb���I�W�A��̧@�Φb��
�q�W�v�C�f���d����N�o�ݪk�[�H�o�i�C�ڭ̤w�g���L�A�L�{���C�ӤƦX�����ѱa�ۤ�
���q��������X�Ӧ��A�o�a�q�������i��O�@�өΤ@�s��l�C
�@�ӥi�`�N���ƹ�O���Ѫ������u�X�{��ⷥ�C����������̤w�g�`�N��o�{�H�A
�ô��X�U�ؤ��P�������C1806�~�A��ù�M���]Grotthus�^�]�Q�o�O�ѩG�������褣
�_�a�b���̤��ѻP�_�X�A�b�ⷥ���A���۾F�������l������ۤϪ������A�b�o���p�쪺
��ݡA�ۤϪ���l�N�Q����X�ӡC
�b�q�ƾǤ譱���̪�o�{�H��A�������y�F�@�Ӯɴ��A���ӡA�j����a�k�Բ�
�]Michael Faraday�A1791��1867�~�^�~���s�B�_�o���D�ӡC�k�ԲĬO�����b�Ӯa�ǰ|
����Ǫ��U��P�~�ӤH�C
1833�~�A�k�ԲĦb�f�º�����ij�U�A��w�@�M�s�W���A�ܤ��٦b�ϥΡC�L����pole
�]���^�o�Ӧr�A�]�����t���ۤެۥ��������[���A�Ӫ���electrode�]�q���^�]������s
���|�^�@���A�N�q�y�i�J���G���@�ݥs��anode�]�����^�A�X�Ӫ��@�ݥs��Cathode
�]�����^�C�ƦX�����ⳡ���A�`�ۤϪ���V�b���G����ʪ��A�s��ions�]���l�^�]io��
�ڥh�^�F���V�������scations�]�����l�^�A���V�������sani��ons�]�����l�^�C�L�S
��electrolysis�]�q�ѡ^�]0�C�@���ѡ^�@���ӥN����ӹL�{�C
�g�L�@�t�C������������A�k�ԲıN�������{�H�k�Ǧ������²�檺���סA�Y�ڭ�
�һ����k�Բĩw�ߡC�]1�^���q�ѽ�ιq�����ʽ�O����A�ѹq�ѩ����X��������q
�P�q�y�j�פγq�q�ɶ�����ҡA���y�ܻ��Y�P�q�L���G���`�q�y�q����ҡC�]2�^�@�w
�q���y�q�����X��������q�P�o���誺�ƾǷ��q����ҡD�Y���P��l�q�A�ӻP�ƦX�q��
��ҡA��Y�P��l������l�q���ƭȦ���ҡF�Ҧp����1�J�B�����A���X�{16��2�Y8�J
�����C�q�L�@���q�y�����X��������q�s���Ӫ��誺�q�Ʒ��q�C�Ҧp1�w�����q
�y�]�YC�DG�DS�D��쪺1��10�^�q�L�ķ��G1��������A�Y��1�D044��10[��5]�J���B�Q
���X�ӡA�p�λ��Q���G�Y��0�D00118�J�Ȥ����X�ӡC�o�ˤ����X�Ӫ��Ȫ����q�ܮe���[
�H��T�����q�A�ҥH��ӳ��⥦�@���q�y����γ��Y�w�����w�q�C
�k�ԲĪ��w�ߦ��G�i�H���Ω�@���q�ѱ��p�F�ۦP���@�w�q�y�q�`�O����X����
�q������C�q�ѥ����ݰ��O��ʪ����l�b�G�餤�a�۬ۤϪ��q��ۤϪ���V�h�C�C�@��
�l�a�@�w�q�����q�έt�q�A��q���ɴN�������l�A�ӥ��h�q���A�u�n�q�ʤO���j�ץi�H
�ӹL�Ϲ諸���ƤO�C��ӻ����i�N�����G�k�ԲĪ��u�@�����A�u�p�G���������O�ѭ�l
�զ������]�A�ڭ̴N���ण�_�w�G�q�]�����@�w���椸�A��@�Υ��M�q����l�@�ˡv�C
�p�����ӡA�k�ԲĪ����礣�������z�q�ƾǤ����ιq�ƾǥH�᪺�o�i����¦�A�ӥB�]
�O�{�N��l�P�q�l��Ǫ���¦�C
�q�y����L�ʽ�
���M��������̪��`�N�D�n�����b���不�q�y���ƾǮ����W�A�L�̤]�S��������L
�{�H�C���[�L�̫K�o�{�F���q�y�q�L����ɽu�ɡA�N�����o�͡A�h��̷Ӿɽu���ʽ��
���P�C�o�ؼ������b�{�����q�O�B���x���譱�A�����j����λ��ȡC�t�@�譱�A1822�~�A
�먩�J�]Seebeck�^�o�{��ؤ��P�����p�������X�u���ɡA�b�䱵�Y�B�[���A�K���q�y
�o�͡C�t�~�@�ӧ��쪺�{�H�O�G�q�y�㦳�Ϻϰw����O�q�C1820�~�A�������ڪ�
�����S�]Oersted�^�o�{�o�@�{�H�C�L�ݨ��o������L�����B���ݩM��L�D�ϩʪ�����
�ӹF��ϰw�C�L�ٻ{�Ѩ�A�L�ΥL��½Ķ�̩ҿת��u�q�Ĭ�v�u�Φ����v�A���ӧڭ�
�{�b�����k�N�O�G�b���Ӫ����q�y�P��Ϊ��ϤO�u�C
�H�̡A�S�O�O�w���]Andre Marie Ampere�A1775��1836�~�^�ߨ�{�Ѩ�����S���[
��G�����n�ʡA�w�����X�A�����ϰw���F�q�y�P�O���@�ΡA�q�y�ۤv�]���۵o��
�@�ΡC�L�ά��ʪ��u��i�����A�Ӭ�s�o�ǤO���w�ߡA�þڼƾ��ҩ��G�@���[��쪺
�{�H���ŦX�H�U�����]�G�C�@����dl���q�y���A���b��~�����@�I�W����cdl sin O
��r2���ϤO�A����c���q�y���j�סAr�O�q�y���P�o�@�I�������Z���AO�Or�P�q�y��V��
�������סC�o�ˡA�ѹq�y�ҥͪ��O�S�k���쥭��Ϥw�ߡA�]���N�P�U���ޤO�κϷ�
���B�q�������O�@�P�F�C�o�S�O���V�u�����z�ǡv���t�@�B�C
�۵M�A�o�عq�y������ι�������X�ӡA���O���Ӧw���������A�N�Ҧ��q�y�椸��
�������[�X�_�ӡA�ڭ̴N��p��X�q�y���ϳ��C
�ھڦw���������A�ڭ̤]���X�ϳ������q�y�Ҩ�������O�C�b�Ů𤤺Ϸ��j��m
�ҳy�����ϤO��m��r2�A�ҥHm��cdl sin �c�C�b�ϳ�H���C�Ҩ�������O�OHm�A�ҥH�b
�Ů𤤦w�����q�y���Ҩ����O��Hcdl sin�c�C�q�o�Ӥ����p���ڹq���W������O�A��
�L�O�ƾǰ��D�Ӥw�C
���Z�q�H�O�q�����ݱo�����H���}�l���C���G�m�����\�h�u�l���x�v�A�O�[�w�o��
���H���^�쪺���C���̴��⮳�}�ڵn�����������t�a�ǹF��F�۴��C�q�譱���C�@��
�s�o�{���P�ϤH�̴��X�@�Ǩϥιq���q�H���N���A���b�w����L��s�q�ϩұo�����G�[
�H���ΥH�e�A�o�ǷN�����S�����G�C�b�w�������G�o���H��A��ھ������o���P��
�ΡA�N�ȶȬO����v���ޥ��P���Ĭɪ��H�����D�F�C
1827�~���k�A�کi�]Georg Simon ohm�A1781-1854�~�^���X�ܦh�^�m�A���U�q�q��
�{�H����ö�X�X�د���T���W�w���q�ӡC�L�ιq�y�j�P�q�ʤO���[���N���F���ɬy��
���u�q�q�v�M�u�i�O�v���ҸW���[���C�q�ʤO�@���۷����R�q�Ǥ��w�g�ϥΪ��u�q��v�C
���i�O�����O�ܰ����ɭԡA�n�N�q�q�@�I�B��L�I�A���ݭn���h���\�A�]���q��t�ιq
�ʤO�i�H�w�q���N�@��쪺�q�Ѥ@�I�h��L�I�ɬ��F�ϧܳo�ӹq�O�ҧ@���\�C
�کi����q����s�O�H�ť߸�������Ǿɪ���s�]1800��1814�~�^���ھڪ��C�ť�
�����]���y�q�P�ūת���צ�����A�M��μƾǤ�k�إߤF���Ǿɪ��w�ߡC�کi�ιq��
�N���ūסA�ιq�N�����A�åB�ι����ҩ��o���[�������ΡC�L�o�{�G�p�q�y�ѥ�S�q��
�թζ먩�J�Ůt�q���y�X�A�q�L�@�ڧ��ê��ɽu�A��q�쪺�����v�O�@�ӱ`�ơC�کi�w
�ߤ@��g�@�G�q�yc�P�q�ʤOE����ҡA
c��kE��E/R�A
����k�O�@�ӱ`�ơA�i�W���Ǿɲv�A�Ө�˼�1��k��R�A�٬��q���CR�u�H���骺��
��B�ūP�j�p�Ӳ��A���P���骺���צ�����A�ӻP���孱�����n���Ϥ�C�o��@��
������q�y�O�b���骺������q�����æa�q�L�C��ӵo�{�A�b�ܰ�������y�q�����ΤU�A
�ٶ��[�@�ǭק�C
�g�w���P�کi���V�O����A�q�y�����D�w�g��F�s���z�Ǫ����n���q�A�]���A����
�q�w�g��X�A�æ��F�T�w���N�q�A�]�ӵ��ƾǤW���o�i���w�F���T����¦�C
�����i�ʻ�
�Q�E�@����~�A�٦��t�~�@�ӥj�Ѫ��[���_���_�өM�T�߰_�ӡA�o�K�O�����i�ʻ��C
�ڭ̻��L�G�����i�ʻ��b�Q�C�@���u���J�J���H�ҽk�D�i�L�A��Ӵf�~�������@��
����T�w���Φ��C���y�ھڨ�Ӳz�ѥ[�H�����C�Ĥ@�A������������v�A�]�����y�H��
�p�G���O�i�ʪ��ܡA���i�]�p�n�i���ˡA�|¶�L��ê�����C�ĤG�A�B�w�۪�����g�{�H
�������u�b���P����W�����P���ʽ�A�Ӧb�Ǽ���V�WŸ�ʪ����i����o�˪��t���C
�������E���]ThomasYoung�A1773��1829�~�^�P���p�����]Augustin Jean Fresnel�A
1788��1827�~�^��o�Ӿǻ��ᤩ��N�Φ��A�ӧJ�A�F�o��ӧx���C���L���@��ƬO�ȱo
�^�Ъ��G���y�H���������C�⻡�����u�̪��L�ɨϥH�Ӥ����ͪ��q�i�C�o�Ӿǻ��P�{��
�ΨӸ����q�l�ʽ誺�z�סA��H�a�ۦ��C
���Ϥ@�����U�����ե��q�L�̤W����Ӱw�աA�A��@�ӫ̩�b�Ĥ@�ӫ̫᭱�C����
�L��Ӱw�ժ����u�b�ĤG�̤W���ۭ��|�ɡA�N���@���C���A�G�����a�X�{�C�o�ǥ��a�O
�ѩ�q��Ӱw�ե����ӨӪ��P�����i���ۤz�A�ӧΦ����C�p�G�@�ӥ��i��F�ĤG�̩Ҩ�
�����{�M�t�@���i�����{���ۮt�ƫꬰ�i�����@�b�A�h�o�@���i���p�P�t�@���i�����N
��n�۹J�A���G�N���Ͷ·t�C�p�G��ӥ��i�e�i�����{���۵��A��̪��i�p�N��n��
�J�A���G�]�N�[���C�ڭ̹�کҬݨ������O�ѥե������@�Ӫi�������үd�U���h����C
�p�G�ڭ̤��Φh��V�����ե��A�ӥγ����@����A�h�ұo���N�O���t�۶��ӫD�m�⪺
���a�C
�ѩҥΪ��������ؤo�H�Υ��a���e�סA�ڭ̥i�H�p��X�U�س������i���C�o�Ǫi
���g�ҩ��O�D�`���u�A��ƶq�Ŭ��@�ɪ����U�����@�A�Τ@�@�̪��G�d�����@�A�M���y
�{�����Ϯg�M���z�g����������۲ŦX�C�Ѧ��i���A�b���u�����|���A�@���ê����
�j�p����i�����פj�o�ܦh�A�ӥB�ƾǤW����s�ҩ��A�p�G�ڭ̰��w�@�ӫe�i���i�}��
���Ѭ��L�ƦP�߰�A����¶�ۻP�H�س̱��i�}���W���@�I�A����A���F���@�I
���P�߰餧�~�A��E���P�߰饲�]�z�A�Ӭۮ��A�]�ӧڭ̲����Ҭݨ����u���u�۪��u��
�Ӫ����C�o�ˡA���t���h�u�u���u�i��A�J�ۻ�ê�����s�����{�H�u����L�p���l�g��
���C
���y���ĤG�x�������p�����ҧJ�A�C�J�J����������i��Ÿ�ʡA�i��P���u����V
�ۥ���A���p�������X�o�Ӵ��ܻ����@�u���b�U��V�W�i����P���ʽ�C�p�G�ڭ̬�
�ݤ@�ӫe�i�����i�}���A�����u��Ÿ�ʫD�W�U���Y���k���C�o�˪��uŸ�������ͩҿץ�
���������C�p�G�@������b�@��m�W�u�����@�Ӥ�V��Ÿ�ʳq�L�A�ĤG���P�˪�����u
�۴��b����90�פ���A���N�q�L�Ĥ@����ӨӪ��������B�_�C�o���O���u�q�L�B���۪�
�{�H�C
���p�����Q�μƾDZN�����i�ʻ��o�i��ܶ꺡���ҬɡC���M�٦��@�ǧx���A���j��
���ӡA�L���������ǻ��P�[���쪺�ƹ겧�`�ŦX�C�L�M�L�H�᪺�H�p��L�B���J�d��
�]MacCullagh�^�_��]Cauchy�^�B�����J���]Stokes�^�B��ܯ����|�J�]Glazebrook�^
���H�g���@�ӥ@���A�~��j�媺�����i�ʻ��T�߰_�ӡC
�p�G���i�O�P��e�i����V�����檺�A�h��C�襲���㦳�ϳo�˪��i��b�䤤�Ǽ�
�����c�C����P�G�鳣����㦳�o�ص��c�C�]���A�p�G���O�����i�ʡA�h�ǥ����H
�ӥ��w���P�T���������ʽ�G�Y�����w�a����ʡC�o�N�O��H�Ӭݰ��O���u�ʪ��T�骺
�\�h�ǻ����}�ݡC��ˤ~�������C��ҥ��ݪ��o�ةʽ�M��P���B�ʨS���J��i�[��
���O���ƹ�թM�_�өO�H�Q�E�@���Y�C�Q�~���\�h�o�����z�Ǯa�������ɤF���ġC���F
�����o�إ��n����ʡA��ӬƦܦ��H�]�Q�H�Ө㦳�^�����������B�ʡC
���p�R�]���Z�ҫ��X���A�����i�ʻ������\�A�b���y���z�Ǥ����}�F�Ĥ@�D�ʤf�A
���M���ɨS�H���D�o�Өƹ�C���y����ݰ��O�b�Ŷ����B�檺�L�ɪ��ǻ��A�M�L���O��
���ǫܬ۰t�X�A�i�O�o�ǷL�ɬ�����u�H�@�Ӥ��ܪ��t�B�ʡA�����F�ѡC������H��
�}�l����ݰ��O�i�ʪ��ɭԡA�A�n�۫H�@����b���F�賣�O�Ѧb����Ŷ��̹B�ʪ��L��
�Ҳզ����A�N�w�g���i��F�C�H�ӬO���F�O�s�����[�I���r�y�X�Ӫ��A�u�n�i�H�����
���O�b�������骺�ѽ褤�Ǽ�������i�ʡA�H�ӴN�����F�o�ӥ��ȡA�i�O�A�p�G���w�H
�ӵL�Ҥ��b�A���w�g�b�Y�طN�q�W�P�Ŷ������X�Ӭ��@�F�C���k�Բī��X�Ŷ��]���q�M
�Ϫ��ʽ�A����J�����ҩ����O�q�Ϫi�ɡA�H�ӴN�����@�w�O���F�C
�����i�ʻ����}�F�{���ҿ׳����z�Ǫ��Ĥ@���C�Ѫk�ԲĩM���J�������u�@�g����
�G���A����P�q���pô�_�ӡC�b�ĤT���̡A�R�]���Z�δX��ǨӸ����U���ޤO�C�]�\��
�@�ѡA�U���ޤO�i��M���P�q�Ϫi�b��j����X���pô�_�ӡC�R�B�y�N�@���b�@�o�˪�
�V�O�C
�q�ϷP��
���R�q���P���ӥͪ��R�q���H�κϥ۹��n�K�������@�ΡA�Ϧ�������̷Q��Q��
��S�q���o�X���q�y�]�\�i�o�P�˪��ĪG�C�Ҧp�k�ԲĴN�Ψ�ڵ��t�u�����۪��Φ���
¶�b�P�@�ڶ�쵩�W�A���O�A���L�ϱj�q�y���_�a�q�L�@�����۽u�ɡA�L�b�t�@���۽u
�̪��q�y�p�W�A�S���o�{��������C
�L���Ĥ@�Ӧ��\������A�b�q�ǥv�W���}�F�@�ӷs�����C1831�~11��24��A�L�V��
�a�Ƿ|�o�˴y�g�o������
��@��203�`�����ɵ���b�@�Ӥj����W�A�A��@�ڪ�203�`���P�˪�������¶�b�e
�@�u��C������A��u���ε��t�u�j�}�A�������ݦ��@�I��IJ�C�@�����۽u�W�s����
�@�ӹq�y�p�A�t�@�����۽u�h�s���b�@�M�q���դW�A�o�q���զ�100����A�C���|��
����A�ӥB�O�����h�ɪ���y���A�R���a�R�F�q�C���q���豵�q�ɡA�q�y�p�W�o�ͬ�M
�����L�p�������F���q�����_���ɭԡA�]�o�ͦP�˪��L�z�����C������S�q�y���_�a�q
�L�@�����۽u�ɡA�q�y�p�W�S��������{�A�Ӧb�t�@���۽u�W�]�S�������P���������A
���M������۽u���o���H�κҷ��W����q�A�ҩ��q���ժ����ʤO�O�ܤj���C
��120������q���ըӭ����o�ӹ���A�]���o�{���O�������A���q�o�⦸����A
�ڭ̬d���F�@�Өƹ�G���q�����q�ɡA�q�y�p���w���L�p����`�`�@�Ӥ�V�F�ӷ��q��
���_�ɡA�P�˪��L�p����h�`�t�@��V�C
��{�b����A�ڥκϥ۩ұo�����G�A�ϧڬ۫H�q�L�@�ھɽu���q���q�y�C��ڤW�b
�t�@�ɽu�W�]�P���Ӳ��ͤF�P�˪��q�y�A�����u�X�{��@�����C����a�����q�ӹy�~��
�q�_���ͪ��q�����ʽ�A�Ӥ����q��S�q���զӨӪ��q�y�F�ҥH����Ϥ@�ڿ��w�ϤơA
�ӫ����v�T�q�y�p�C
�o�ӹw�������G���o��F�ҩ��C�]������¶�b�����ޤW�����ߪ��p���۽u�ӥN���q
�y�p�A�S�b�o�����۽u�̦w�ˤ@�ڿ��w�A�A�p�e��P���u��M�q���ճs���_�ӡA�b�q��
���_�H�e�N���w���X�A�ڭ̵o�{���w�g�ϤƤF�C
�p���q�F�q�A�M��A��@�ڤ����Ϥƪ����w�w��b�p���۽u���A�̫�A��q�����_�A
�ڭ̵o�{���w���Ϥƫת����W�M�H�e�@�ˡA���O�����ⷥ�o�P�H�e�ۤϡC
�β{�����F�ӹq�y�p�A�ڭ̫ܮe�������k�ԲĪ�����C�u���Τ@�ӥ�S�q���@����
�q�y�A�Өϭ�q���P�ƹq���@�۹諸���ʡA�ΥΤ@�ӥú��K�M�@�ӻP�q�y�p���p���u��
�@�۹ﲾ�ʡA���i�H�ҩ����P�˪��Ȯɹq�y���o�͡C�k�ԲĹq�ϷP�����o�{�A����Ӥu
�~���j�o�i���w�F��¦�C�t���h�@����ΤW���n���q�O�����A���O�ھڷP���q�y����z
�s�����C
�q�ϤO��
�w���o�{�q�ϩw�ߡA�μƾǤ����⥦���F�X�ӥH��A�N�P�캡���A�S���A�h�����o
�ؤO�a�������Ǽ��F�C�����~�L���k�ԲġA���O�ƾǮa�A����Ŷ��ιq�ϤO����
���z�ʽ�P���A�S�O�P�쿳��C�p�G��@���Ȫ���b�ϱ����W�A�A���@���K�h���G�b��
���W�A�o���K�h�N���X���\�h�u�A�����ϤO�O�u�o�ǽu�Ӱ_�@�Ϊ��C�k�ԲķQ���o�˪�
�O�u�ΤO�ޱN�Ϸ��ιq���s���_�ӡA�u���s�b��ϳ��ιq�������A���̤]�\�O���ƤF��
���I�Ҳզ�����C�p�G���̶H��ֱ����ˡA�B�b��i���A���U�A�V�a����V�Ԫ��A�ӦV
���V���Y�A���̷|�b�ѽ褤���i�X�h�A�ӱN�Ϸ��ιq���V�@�_���l�A�o�˥i�H
�����l�ު��{�H�C����ڬO�_�o�ˡA�Ϊk�ԲĪ��O�u�A�Ӫ��ܵ��t���C��ιq������
���O�P���ܪ��{�H�A��b�O�@�ӫK�Q����k�C
�k�ԲĤS�q�O���譱��s�F�q���誺���D�C�L�o�{�b����P�Ů��ν��β��@
�����t��ҥN���ɡA���骺�R�q�e�q�A�Y�b�@�w�q��ιq���U����t�����q�q�A�K���W
�[�F�o�ӼW�[����ҥL�s�����ӵ��t�骺�q�e�v�C
�k�ԲĪ����ѶW�L�F�L���ɥN�A�ӥB�L�ΨӪ��F�o�Ǩ��Ѫ��N�y�A�]���O���ɩҼ�
�ߪ��C�T�Q�~��A���J�����N�o�Ǩ���½Ķ���ƾǪ������A�õo�i���q�Ϫi���z�ɡA
���̪����n�ʤ~�Q�H�{�ѡ]�b�^��ߨ�N�Q�H�{�ѡA�b��L��a����C�^�C�o�ˡA�k��
�ĴN���w�F��ιq�Ǫ��T�j�����A�Y�q�ƾǡB�q�ϷP���P�q�Ϫi����¦�C�ӥB�L���M�D
�i�q�ϤO���㦳���j���n�ʡA�o�]�O�{�N�����z�Dzz�צ����q���譱�����v�_�I�C
�q�ϳ��
�ڭ̱o�P�¨��w�ꪺ�ƾǪ��z�Ǯa�����]1777��1855�~�^�P���B�]W�DE�DWeber�A
1804��1891�~�^�A�]���L�̵o���A�@�M��Ǫ��ϻP�q�����C�o�س�줣�O�ھکM����
�P�����q���N��w���A�ӬO�ھڪ��סB��q�P�ɶ��T�ذ��Ө�w���C
1839�~�A�����o���F�L���m���ӶZ������Ϥ�ӧl�ު��O���@��z�סn�@�ѡC�q���B
�Ϸ��H�θU���ޤO���A�X�o�����Y�C�o�ˡA�N�i�H�����j�ת��q���κϷ��U�o�˪��w
�q�G�P�۵��������q���κϷ��b�Ů𤤬۶Z�@���]1���̡^�A�ӥH�@��쪺�O�]1�F�]�^
��ӹq���κϷ��[�H�ƥ����q���κϷ��C�p�G�Υt�@����ӥN���Ů�A�o�ӤO�N���@�w
����Ҵ�֡A�L��k�ӥN���q�O�Au�N���ϤO�Ck�N�O�k�ԲĪ��q�e�v�A�b�o�̦�������
�`�ơAu�o�Ӷq��ӥs�����誺�Ͼɲv�C�b�o�Ӱ�¦�W�����إߤF�@�ӧ������ƾǺtö
���j�H�C
�w���P���B�ѹ����ҩ��a�q�y���u��A�P�P�j�p�P�Φ������K���@�άۦP�A�@�Ӷ�
��q�y�P�@�Ӧb����V�W�Ϥƪ���L���ġA�ҥH�@���O���_���A�t�@���O���n�����C�o
�˳��q�y�i�w�q���M���ϤO���ϽL���Ī��q�y�C�ھڳo�өw�q�A�i�H�μƾǤ�k��
�X�p�U���G�G���q�y���ߪ��ϳ��]�Y�@�Ω���Ϸ����O�^����2xc��r�A�o��c�O�q
�y���j�סAr�O��骺�b�|�A�o�Ӻ⦡�۵M�P�Ѧw�������ҾɥX�����G�ۦX�C�ҥH�u�n
�N�@���p�ϰw�a���b�@�j��u�骺���ߡ]�o�ظ˸m�N�O�{���һ��������q�y�p�^�A�A��
�q�y�q�L�u��ɡA�[���ϰw������A�ڭ̴N�i�H�H����������̤@�J-���]C�DG�DS�D�^
���h���q�q�y�C�`�Ϊ��q�y���]�w���^���W�w�O�W���һ�����쪺�Q�����@�A���L�A
�h�~�H�Ӭ��F������λP���q�K�Q�A�@���O�ھڹq�ѮɪR�X�Ȫ����q�Ӱ��q�y��쪺��
��A�p�W���ҽͨ쪺�C�{�b�S���H��ij���^��z�ת��w�q�W�h�C
���P��q�u��
�b�Q�K�@���M�Q�E�@�����A�ѩ�]�T�����o�i�A���Ǧ����@���㦳�D�`���n�����
�N�q����ǡA�o�ϹL�Ӥް_�H�̹����Dzz�ת����s�`�N�C
�ڭ̥H�e���L�A���Ӽ��軡�A���O�@�ؤ��i���q���y��C�o�Ӿǻ��b�ҵo�M������
�q���q������譱�_�L���q���@�ΡC���@�����z�������A���l�E�ʻ���X��ӾU���۵M
���Ǯa�p�i�q�թM���y���f���C1738�~�A�O���V�Q�]Daniel Bernouilli�^���X�A�p�G
�N����Q�����V�|���K��B�ʪ����l�A�����o�Ǥ��l�ﲱ���������R���A�K�i��������
�����O�A�o���O�S���]����Q���Y�P�ūת��W���ӫ���ҼW�[�A���p����ҭn�D�����ˡC
����ת̸��������ͼ����{�H�ɡA���w�����ͥX���h���μ�����̲A���D�n����
����������H�e����A����n�p�@�ǡA�]�Ӽ��O�Q�G�X�Ӫ��{��~���C���b1798�~�A
����H�������]Benja-min Thompson��Ӧb�ڥ�Q�Ȧ��F�Ժּw�B��Count Rumforo�^
���p�����������ҩ��o�����q�j�P�P�ҧ@���\���`�q������A�ӻP�d�����q�L���C�i�O
�����y�黡���M�s�b�F�b�ӥ@���C
���L�A��1840�~�A�H�̴N�}�l�F�Ѧ۵M�ɸ̦U�د�q�ܤ֦��@�ǬO�i�H�����ܴ����C
1842�~�A�ں��]J�DR�DMayer�^�D�i�Ѽ��ܥ\�Υѥ\�ܼ������i��C�ں��b�Ů�Q���Y
���ɭԡA�Ҧ����\�����{���������w�U�A��X�F����������q���ƭȡC�P�~�A�^����P
�x�ݬ�Ǯa�B�H�o���@�إ�S�q���ۦW����ù�ҡ]W�DR�DGrove�^��h�A�b�@�����t��
�����F�۵M����q�ۤ����Y���[���A�æb1846�~�X���@���ѡm���z�O���ۤ����Y�n���A
�ĭz�F�o���[���C�o���ѩM1847�~�w��j�Ͳz�Ǯa�B���z�Ǯa�P�ƾǮa�����i�N��
�]H.L�DF vonHelmholtz�A1821��1894�~�^�ھڿW�ߪ���s�g�����m�פO���u���n�A�O
�@��a�z�{���ҿת��u��q�u���v��z���̦��ۧ@�C
1840��1850�~���A�J�ա]J.P.Joule�A1818-1889�~�^�H�����k���q�F�ιq�M����
�\�ҥͪ����q�C�L���ҩ��q�y�q�L�ɽu�ҥͪ����q�A�P�ɽu���q���M�q�y���j�ת�����
������ҡC�L�����q�L���ީ����Y�@�w�q���Ů�ΨϽ��l��ʩ�G�餤�A�ӨϲG��ͼ��C
�L�o�{���ޥΤ���覡�@�\�A�P�q���\�`�o�P�q�����A�ھڳo�ӵ��Ȫ���z�A�L�_�w��
�O��q���@�اΦ��C���O�o�ˡA�u�g�L�h�~����A��Ǭɻ�S�~�}�l�٦P�o�جݪk�v�A
���M�����J���i�D�·G�E���i�͡]William Thomson�^�G�u�L���@���J�ժ��@�ӫH�{�v�C
1853�~�A�����i�N���X�ݭ^��ɴN�w�g�ݨ��\�h�H��o�Ӭ�ǰ��D�o�Ϳ���A�L��k��
�ɤS�ݨ��p�����]Regnaull�^�w�g�����F�s���[�I�C�J�ժ��̫ᵲ�G�����G�Ϥ@�S���b
�ؤ�55��60�פ����ūפɰ�1�שһݭn���Ӫ��\��772�`�S�C��ӹ����ҩ���������T
���Ʀr�O778�`�S�C
�J�եμ��P�\���������T�����絲�G�A������ù�ҩҥD�i���u�O���ۤ����Y�v�B�M
�����i�N���ҭҾɪ��u�O���u���v���[���H���O������C�o���[���N�o�˵o�i�������z
�ǤW�H�u��q�u���v�o�W���T�w��z�C��q�@���@�ӽT�������z�q�A�b���ɪ���ǤW��
�O�s�F��C�o�ӦW���Ҫ��ܪ��[���A���g�Τ���T���B�㦳�����N�q���u�O�v�@���Ӫ�
�F�C�������E�����X�A�o�˴N��u��q�v�M�u�O�v�V�c�_�ӤF�C��q�i�H�w�q���u�@�\
���O�v�A�ӥB�p�G��̪��ഫ�O�������A��q�K�i�H�Ωҧ@���\�Ӵ��סC�u��q�v�@��
�Ω�o�رM�����N�q���k�\�������]Rankine�^�P���i�͡C���i�ͪ��ΤF�������E����
���X����O�M��q�ϧO�}�Ӫ��D�i�C
�J�ժ������ҩ��b�L�Ҭ�s�L�����p�̡A�@����t����`�q�O�u�����A�\�үӥ�
���q�A�Y�@�����ӥX�{�C�@�몺�Ҿڤɧڭ̧�o�ӵ��G���s���L���ܤƤW�h�A�Ҧp
������ܬ��q��A�Τƾǯ��ܬ��ʪ��������C�����~����A�@���w�����ƹ곣�A�X��
�o�y�ܡG�b�@�өt�ߪ���t���A�`����q�O�u�����C
�o�˽T�ߪ���q�u����z�i�H�M��������q�u����z�۷B���C���y���ʤO�Ǫ���¦
�N�b��o�ˤ@�ػ{�ѡG���@�Ӷq�A�w�w���F�K�Q�_���A�٬��@�Ӫ��骺��q�X�X�g�L�@
���B�ʦӤ��ܡC�b�ƾǮa��̡A�ѯ��ҩ��G�o�ӭ�z�b�ƾ��ܤƤ��]�@�˦a���ġC�b��
�𤤿U�N������A������q�ä������C�p�G��Ҳ��ͪ����覬���_�ӡA���̪��`�q����
��쪫��P�үӪ��Ů𪺥��q���`�M�C
��q�]�O�o�˪��G��q�H�~���t�@�Ӷq�X�{�b�ڭ̪��N�Ѹ̡A�D�n�O�]�����g�L�@
�t�C���ഫ���M���ܡC�ڭ�ı�o�ӻ{�o�Ӷq���s�b�A�⥦���@�@�Ӭ�Ǫ������A�åB��
���_�@�ӦW�r�A�O���غثK�Q���C�ڭ̺٥�����ί�q�A�Ωҧ@���ʶq�εo�ͪ����q��
���q�����ܤơA�åB�O�F�\�h�u�ҡA�g�L�\�h�ôb�A�~�o�{�����u���ʡC
�Q�E�@�������z�ǡA�S���@�Ӥ�k�i�H�гy�η�����P��C�G�Q�@���X�{�F�@�Ǹ�
�H�A�����襻���N�O��@�اΦ��A�q�誺�Φ����ܬ���Φ��ëD���i��ơA����
���Ǧ~����A��P��O�I�M���P���C
��q�u������h�A���b1853�~�����i�ˡ]Julius Thomsen�^�������Ω�ƾǡC�L�{
�Ѩ�b�ƾǤ����̩ҵo�X�����O�o�Өt�Ϊ��X��q�b�����e�᪺�t�����Ŷq�ثסC�J�M
�b�@�ӳ��X���t�Τ��A�̫᪺��q�M�̪쪺��q���M�O�ۦP���A�]���A�b�Y�DZ��p�U�A
�ڭ̴N���i��w���o�Өt�Ϊ��̫᪬�A�A�Ӥ����U�Τ������B�J�A�]�N�O�@�B����@��
���z���D���ѵ��A�Ӥ������s�F��ؼЪ��L�{�A���f���Y�Ǥ���������O�ǰ��D
�Ұ��L�����ˡC�ѩ�o�ӹ�ڪ��γ~�M���T�����N�q�A��q�u����z�i�H�ݰ��O�H����
�F�����j���N���@�C
���O�����ۤv�����ǤW���M�I�ʡC�ѩ��q�u����z�M��q�u����z�b���ɥi�H��
�s���@�����p�U�L�����ġA�o��ӭ�z�N�ܮe���Q�ަ������M���w�ߡC��q���F�ë���
�������F�t�z�̪���q�A�b�@�����ΤU�Τ@���ɶ��������F�u���Ӥ��ܪ��C�o�ǭ�z��
�A�O�ɤH�̦b���ѻ�줺�̭ɸg��v���e�i���U�L�@�����T�ɡA�Ӧ��F���ĩʥi�ê�
���n���DZ�F�C
����B�ʻ�
1845�~�A�˯S���y�]J�DJ�DWaterston�^�b�@�g��Z�Ƨѿ����A�i�@�B�o�i�F�ѩ�
���P��Τ@�_�Ӧ���o��[���n������B�ʻ��C�o�g�Ƨѿ��b�Ӯa�Ƿ|���ɮ����m�h�~
�ӳQ�H��ѤF�C1848�~�A�J�դ]��s�F�o�Ӱ��D�C�o����Ǯa��o�Ӳz�ױ��i��O��
�V�Q�ҨS���F�쪺�a�B�A�åB�U���ۿѦa��X���l�B�ʪ������t�סC1857�~�A�J�ҭE��
�]Clausius�^�~�����o���F���T������B�ʻ��C
�ѩ���l�I�������|�ܦh�A�ӳo�ظI���S���w�a���������u�ʡA�ҥH�b���������A
�Ҧ������l���w�V�@����V�A�a�ۤ@���t�צӹB�ʡC�������l�������`��q�i�H�q�o��
�骺�`���q�A�ӨC�@���l��������q�i�H�q�o�ūסC�q�o�ǫe���A�ڭ̥i�H�μƾǤ�k
���ɥX���骺���OP����1/3nmV2�A�o��n�O���e�n�������l�ơAm�O�C�Ӥ��l����q�A
V2�O����t�ץ��誺�����ȡC
��nm�O���e�n�����骺�`��q�A�Y�O�����K�סA�ҥH�p�G�ūשMV2���ܡA�h����
�����O�P��K�צ�����ҡA�λP��e�n���Ϥ�ҡA�o�O�i�q�եѹ���o�{���w�ߡC�p�G
�ū��ܤƪ��ܡA�ѩ�p�PV2����ҡA���O���H�ūצӼW�[�A�o�N�O�d�z�w�ߡC�p�G�ڭ�
����خ���b�P���P�P�Ť��U�A�q�H�W����{���i���b���e�n������骺���l�Ƭ۵��A
�o�O������wù�q�ƾǨƹ�o�쪺�w�ߡC�̫�A�N�o��خ���ӻ��A���l���t��V���w
�P�K��nm������ڦ��Ϥ�ҡA�o���Y�i�H�������麯�z�h�ն������t�סA�o���O1830�~
��p�̩i�]Thomas Graham�^�ѹ���ҵo�{���w�ߡC
�q�o�Ǻtö�i���O���V�Q�B�J�թM�J�ҭE�������X����B������B�ʽשM���骺��
��²�檺����ʽ�O�ŦX���C�ӥB�p�˯S���y�M�J�թҪ������A�o�Ӿǻ��ϧڭ̥i�H��
���a��X���l���t�סC�Ҧp�A�b���s�פΤ��ȬW760�@�̼зǤj�����A�ΨC��������1�D
013��106�F�]�����O�U�A�B������q���e�n�O11�D16�ɩ�11.160�ߤ����̡C�]���qP
��1/3nmV2��{���o��V���C��1844�̡A�ΨC���@�^���h�C���������Ʀr�O�C��461
�̡C�o�ǼƦr�OV2�������Ȫ�����ڡFV�����������ȡA�Y���l�t�סD�y�p�@�ǡC1865
�~�A�ҬI�̯S�]Loschmidt�^�ھڮ���B�ʽסA������X�@�ߤ����̪�����b0�vC�M�j
�����U�Ҧ������l�ƥج�2�D7��1019�C
���J�����P�i�����ҡ]Boltzmann�^�N�����ѷ��v�z�שҾɥX���~�t�����Ψ�t��
���t�����D�W�h�A�o�Ӳz�ײ{�ɹ�\�h��s�������Q�����n�C�������ѩ���l�����M�I
�������|���h�A���̥i�����X�s�A�C�@�s�b�Y�@�t�d�B�ʡA����G�p��5�ҥܡC
��ХN���t�סA�a�ХN���H�Y�@�t�B�ʪ����l�ơC�p�G�H�̥i��t�����A�ڭ�
�N�i�H�ݥX�A�t�פT����̥i��t�ת����l�Ʈt���h�i�H���Ӥ��p�C�H���٥i�H���X��
�������u�Ӫ��ܹv�W�j�u���G�A���z�q�פ����~�t���G�A�������B�魫�B�ةR���u�B��
�Ҹդ����{�X����O���������H�s�����G�C���צb���z�ǡB�ͪ��ǩΪ��|��ǤW�A���v
�z�P�~�t���u�����ܤj�����n�ʡC�w���@�ӤH���ةR���u�Τ@�Ӥ��l�b���ӬY�ɨ誺
�t�סA�O���i��F���p�G���F�����ƥت����l�ΤH�A�ڭ̴N�i�βέp����k�ӥ[�H�B
�z�A�ڭ̥i�H�b�����U���d�A�w�����n�h���l�b�Y�@�t�d�B�ʡA�Φn�h�H�N
����Y�~�C�q���ǤW�ӻ��A�ڭ̤������ڭ̤w�g�F��@�زέp�M�w�סA���M�b�o�Ӷ��q
�̡A���骺���T�w���M�s�b�C
�i�����һP�U�ˡ]Watson�^�d���D��ӥH�L�سt�B�ʪ����l���k����J�����Ъi
�����Ҥ��G���ɦV�F�]���o�O�̥i����G�C�L���ҩ��o�ضɦV�P���O�ǤW�@�ӦW��
�u�i�v���q�ͩ�̤j�Ȫ��ɦV�۷��C�F��o�س̥i����p�X�X�Y�i�F��̤j�ȡA�t��
���~�t�w�ߤ��G���L�{�A�M�~�ȵP�ۦ��C�o�ز{�H�b�۵M�ɸ̬O�H�ɶ��������۵M�X�{
���F�{�ɦb��ǤW�M���ǤW�A�������j���n�ʡC
���J�����٫��X���骺�ߺ��ץ��̨䥭���ۥѵ{�өw�A�ҿץ����ۥѵ{�Y�@���l�b
�⦸�I�������Ҹg�L���������{�C�B�������ۥѵ{����17��10[��6]���̡A��8�D7��
10[-6]���̡C�I�����W�v�����C��10[9]���A�o�ӼƦr�ܤj�A�������������M���l���t
�ܤj�A���骺�j�����M�ܺC�C���骺�ߺ��רä����@��H�ҷQ���������H�K�צ��ܤp�A
�ӬO�H�ۮ��骺�Q��X�A�l�O�����ܡA���D�K�F��ܧC�������C�o�Dzz�ת����G��
������ҩ��A�]���o�Ӳz�ת�������`�������ܦ��N�o��H�̪��H���C
�ھڮ���B�ʽסA�ūO�Τ��l�����ʪ�������q�ӫq���A���o�Ǥ��l�]�i���
������ʡB���ʵ��ӨӪ���q�C���J�����M�i�����Ҫ����`��q���P���l���u�ۥѫת�
�ƥءv�A�Y�M�w�@�Ӥ��l����m�һݭn�����мƦ���ҡC�Ŷ��@�I����m�M�w��T�ӧ�
�СA�]���M�w�ūת����l���骺�B�ʡA�t���T�ӦۥѫסC�]�ۥѫת��`�Ƭ�n�A������
�����ɡA����@����3��n�ܬ����ʪ���q�A�H�ϷūW���A��E�]n��3�^��n�h�Q��
�l�Ψ��L�B�ʤW�h�C����b�e�n�u�������p�U�[���ɡA�Ҧ��������ΨӼW�[���l����
�q�A���p���O���ܡA�e�n���W�[�A�]�������ϧܤj�����O�ӧ@�u�C�ڭ̥i�H�ҩ��A�q
�o�̥i�H���X�p�U���סA�b�w���M�w�n�����p�U�A��ؤ������y�i�H����1��2��n�C��
�H�A�pn��3�AY��1��2/3��1�D67�C�b���J�����i��o�ӭp�⪺�ɭԥL�٤����D�������
�馳�o�˪���ȡA����ӵo�{���l�U���l������A�p�E�]��B��M�X��o�ӭp��
���G�A�]���A�N����l���ӽסA���̻P²�檺���I�õL���O�C���`������p�B�P��O
����l�����l�C���̪��^����1�D4�A�����o�Ǥ��l�����ӦۥѫסC
�p�G�N�ūת����ܤ@�֥[�H�Ҽ{�A�i�q�թw�ߢw�wpv�ױ`�ơX�X�i�X�i��pv��RT�A
P�O�@�ӱ`�ơC���l�����l�ޫ��K�ת�����a��v2���ܤơA�o��a�O�@�ӱ`�ơA�ҥH�A��
�ĪG�Np�W�[��P��a��v2�C���l�����ҥe���e�n�A����A�[���Y�A�ҥH��ĪG�Nv�Y���
v��b�C�]���A�S�E�w�E�˺����]Van der Waals�^��1873�~�o��H�U����{���G
�]p��a/v2�^�]v��b�^��RT
�o�Ӥ�{���ΨӪ��F�Y�ǡu�D�z�Q����v�A�P�i�q�թw�ߦ��X�J�����p�A�ᬰ�X�A�C
���X�쪫�z�Ǯa�A�S�O�O�w�w�|���]Andrews�^�A�ι����k��o�خ���[�H�ҹ�C
�w�w�|���b1859�~���k�����P�G���ت��A���s��ʶi��F��s�C�L���X�C�خ��鳣
����T�w���{�ɷūסA�b�o�ūפ��W�A�L�����O��ˤj�A������ϳo�خ���G�ơC�]��
����G�ƪ����D�O�@�ӫ�˧�ū��C���{���I�H�U�����D�C
�Ӫ��Ǯa���ԡ]Robert Brown�^1827�~�b��L��U�ݨ����L���I�����W�h�B�ʡA�q
�Ӫ����ҩ��F���l���B�ʡF1879�~�ԩi�ɡ]William Ramsay�^�b�����o�Ӳ{�H�ɡA�{��
�o�O�ѩ�G����l�R���a��G�餤�����I�ӳy�����C�J�|�J���]Crookes�^�`�N��p�N
���������l�@����¡A�˸m�b���ׯu�źޤ�������b�W�A�A�⥦��b������A��������
�G���@������V����C���J�����b�����o�ر���ɻ{���o�O�ѩ�ª��@���l���F���h��
���ӳy�����C���l�����E�ʡA�H�������t���D�A�I�������l�ɡA�K�N���V����ʡC
���O��
1824�~�A�u�ӧQ����´�̡v����l�d�ա]SadiCarnot�^�A���X�C�@�����]�μ������^
�������@����μ����P�@�N��ΧN�����A�������u�@�ɡA���Y�Ѹ���������Ǩ���N��
����C�d�զb���Z���ͨ��q�������[���A�����ܪ��ɶ��A�H�̳����Ӽ��軡�h�F��
�L����s���G�A�H�����g�L������b�q�W����A�O�a�ūת����C�ӧ@�u���A�������а�
�B�����A�Ϥ����u�@�@��C
�d�ջ{���n��s�������w�ߡA���������Q����²�檺���ΡF�������L�����A�����|
�]�ǾɦӴ����C�L�ٻ{�Ѩ�b��s�������u�@�ɡA�ڭ̥������w�����q�L�@�ӧ������[
��`���A�@�u������A�L�O�]�T�]�n���Y�Ů�]�n�Ψ�L����F��]�n�A�g�L�u�@
���ᤴ�M�^�_���Ӫ��A�C�p�G���O�o�ˡA�����i��q�u�@���褺������q���l���ʩ�
���A�������\�i��N�����O�g�L�������~�������Ұ����F�C
�d�ժ��`�������{�N�Φ��O�J�ҭE���P���G�E���i�͡]�Y��Ӫ��ͺ���k��^����
���C���\�ܦ����μ��ܦ��\���ɭԡA�䶡�����Y�i�H�εJ�ժ����G�Ӫ��ܡC���L���M��
�����i���@�w�q���\�����ܦ����A�ϹL�ӭn��@�w�q���������ܦ��\�A�@��ӻ��o�O
���i��C�b�]�T���Ψ�L�����̡A�Ҩ��������q�u���@�p�����ܦ������A��E����
���Ѿ��������������Ǩ���N�����A���వ���Ϊ��\�C�g���ҩ��G�����}�ʮɱq������
�Ӥ@�w�q����H�A�ӧ�䤤���@�������qh�ǵ��N�����C�o��Ӽ��q���t�]H��h�^�N�O�i
�ܬ��\W���̤j���q�A�ӹ�ڧ������\�P�ҧl�������q����W��H�A�i�@���o�Ӿ�������
�vE�C
�@�Ӳz�פW�����������A�J���|�ѶǾɥ��h���A�]���|�Ѽ������h�\�A�ҥH
W��H��h�A
��E��W/H��[H��h]/H�C
�@�������������㦳�ۦP���IJv�A�_�h�A�ڭ̫K�i���Ӿ����s���b�@�_�A�q�N��
�������त�o��\�A�γq�L�@�ئ۰ʪ�����A�~���_�a��q�N��l����餤�h�A�o��
�̳��O�P�g�礣�X���C�]���A�IJv�H�ΥѼ���l�������P�N���X��������A�O�P����
���Φ��Τu�@���誺�ʽ�L�����C�M�o�Ǽƶq�������u���������ū�T�M�N�������ū�t�F
�ӧl�������P��X��������A�u�n�g���FT��t��H��h�F���Φ��ɡA�K�i�ΨӰ���ӷū�
���w�q�A��O�G
E��(H��h)/H��(T��t)/T�C
�o�ˡA���i�ʹN��w�X�@�ؼ��O�Ǫ��żСC���O���諸�A�]�����P�������Φ��Τu
�@���誺�ʽ�L���C�p�G�@�ӧ����������N�������ūO�s�סA�Yt��0�A��E��1�A���N
�O���Ҧ��l�������ܬ��\�A�S������N�����h�A�o�ɮIJv�O1�C�����������@�l
���������q��h���\�A�Ϊ̻�����������IJv������j��1�C�]���o�طżЪ��s�O��
��s�סA�Y�S����o��N���ūפF�C
�o�˳W�w�����O�Ǫ��żСA�º�O�z�פW���C��ڤW�A�ڭ̮ڥ��L�k���q�@�ӧ���
�����ҧl�������q�P�ҩ�X�����q����A�Ӥ���o��ӷūסC�满�@�Ӳz�ѡG�ڭ̮ڥ�
�L�k��y�X�@�ӧ����������C�]���ڭ̥�������O�Ǫ��ż��ܦ���Ϊ��F��C
�J�զb�@�Ӭ�s�̡A�M�L�H�e���ں��@�ˡA�Q�ι�Ů�i�����Y����k�ӧ�\�ܬ�
���C���L���F�����L���γo�ӿ�k���z�ѡA�J�խ��s�i��F�\��Чf�ħJ���Q�ѰO�F��
����A�åB�ҩ����ŮȦӤ��@�u�A�h�ūרS���iı����ܡC�Ѧ��i�������鿱��
�Φ��Y���ɭԡA���骺���l���A�S�������ܤơA�b���Y�Ů�ɡA�ҧ@���\���ܧά����C
���i�ͻP�J�ճ]�p�F�@�ӧ��Ӫ������k�A�ҩ��N�������L�@�Ӧh�ժ���A�M�����
�ۥѿ��ȡA�ūת����ܹ�b�����A�Ů�y���ܧN�A�B��Ʀܵy�y�ܼ��C�ھڼƾǤW����
�{�i�H���D�A�p�G�ΪŮ�βB��s���ūp�]�s�ױ����273�J�^�A�o�طūp�t���h
�M���諸�μ��O�Ǫ��żЬۦX�A�䶡���p�p�t���A�i�H�q�ۥѿ��Ȫ����ĪG�p��X�ӡC
���O�ǤW�����z�ұo�X�����סA�����Ϥu�{�v�i�H������z�ש�b���ꪺ��¦���W�A
�ӥB�b�\�h�O���譱�j�j���ʤF�{�N���z�ǩM�ƾǪ��i�B�C�k�Բij��Q�����O�A�N�b
�@��²��������N���G�ƤF�C������żЪ��z�ץH�δ��i�ͩM�J�ժ��h�ն���笰�{
�N���@�t�C��s�}�P�F�D���C�g�L�o�@�t�C��s�A�ש�Ϥ@���w�p���鳣�G�ơA�åB��
���ҩ��U�����������賣�b�T�ت��A�U�s��s�b�C�h�ն몺�ĪG�b���`�ūפU�T�M�ܤp�A
�b��������N�o�H��A�N�ܱo�ܤj�C�p�G���_���Ϥ@�اN����q�L�@���L�A���|��
�o��N�A�åB�i�H�ΨӧN�o�᭱�y�Ӫ�����C�o�ˡA�o�ӹL�{���ĪG�N�ֿn�_�ӡA����
�̫�N�Q�N�o���{�ɷūצӲG�ơC���ˡ]James Dewar�^��h�b1898�~�γo��k�ϲB�G
�ơA�d���L-�Τ����]Kamerlingh��Onnes�^�b1908�~��̫�ѤU�Ӫ����G�ơC���˥�
�Ӷi��G�ƹ��窺�u�Ŭ����~�A�N�O�{���H�Ҽ��ߪ��Ť��~�C
�����֤H��s�L�o�ط��C�Ź����ʽ誺�����C����۪��@���ܤƫK�O�q���Ǿ�
�v����@�W�j�F�Ҧp�]�b�G�A�ūס]��268�D9�J�^���ɹq�v��b0�J�ɡA���j�Q��
�]109�^���C�q�y�b�o�اC�Ū����ݹq���̡A�@�g�}�l�A�ϸg���\�h�p�ɦӤ��y��C
�n�q���������o�즳�Ϊ��\�A�Ůt�O���ݪ��C���b�۵M�ɤ��A�q�L�����ǾɻP��L
�覡�A�Ůt�O���_�ܤp���C�]���b�@�Ӧ����i�f�����ܶi�檺�t�ߪ��t�Τ��A�i�@����
���\������ɦV���_�a�ܱo�U�ӷU�֡A�Ϥ��A�J�ҭE���٬��i���ƾǨ�ơ]�b�i�f��
�t�Τ��O�`�ơ^�A�o�ɦV��W�[�C���i�Ϊ���F��̤p���ש��i�F��̤j���ת��ɭԡA
�N�A�S���\�i���F�A�o�˴N�i�H�T�w�o�Өt�Ϊ����ũҥ��ݪ�����C�P�ˡA�b�@�ӵ���
�]�Y�ūפ��ܡ^���t�Τ��A���N�����]Willard Gibbs�^�ҳХߪ��t�~�@�ӼƾǨ�ơG
�u���O�Ǫ���աv��F�̤p���ת��ɭԡA�]�i�H�F�쥭�šC�o�ˡA�J�ҭE���B�ͺ���B
�����i�N���B�N�����P�`�����S�]Nernst�^���N�ХߤF�ƾǩM���z�ǥ��Ū��z�סC�{�N
�����z�ƾǪ��ܤj�@�����A�H�γ\�h�u�~�W���n���N���γ����L�O�N�������O�Ǥ�{
�����@�t�C��������ҦӤw�C
�̦��Ϊ����G���@�N�O�ҿת��۫ߡC�]�Q�@�t�θ̦�n�Ӥ��P�������]�Ҧp���P�Q
��Ӧ����^�Mr�Ӭۡ]�Ҧp��ӹ���B�@�ӹ��M���G�M�@�ӻ]�T���|�Ӭۡ^�A�ھڦN��
���w�z�A�ۥѫת��ƥ�F�N�On��r�A�o�W���ٶ��[�W�ūP���O��ӦۥѫסC�]���۫�
�i�����U���G
f��n��r��2
�H�e�o�{���ĤG�Ӥ�{�����X�p�U�|�Ӷq�X�X�Y���A�ܤƪ����L�A����ū�T�A
���Op�P�e�n���ܤ�u2��u1�X�X���������Y�A�Y
L��T(dp/dT)�]v2��v1�^��dp/dT��L/T�]v2��v1�^�C
�o�Ӥ�{������z���ӬO��i���E���i�͡]James Thomson�^�ҳХߪ��A1850�~��
�k�A�ѳͺ���k��B�����M�J�ҭE�����H�[�H�o�i�A�H��A�ѰǡE�L�S�Q�J�]Le
Chatelier�^���Ψ�ƾǰ��D�W�C�����{�P�۫ߤ�{�X�b�@�_���ѤF���P���۪�����
���@��z�סA�H�Ψt�Τ����Ů����O�H�ūת��ܤƲv�C�Ѧ��]�i�H���D�A�~�ɹ�t�Ϊ�
�@�Φb�t�Τ��y���@�ع�ܪ��ϧ@�ΡC
�b�۫ߤ�{�̡A�pr��n��2�A�hF��0�A�o�Өt�ΫK�O�u�D�ܨt�v�C�Ҧp�A�b�u���@
�Ӧ��������p�U�A�����誺�B�B��M�T�T�۶��b�@�_���ɭԡA���̥u���b�Y�@�S���ū�
�~��F�쥭�šA�ӥB�u���b���O�վ��Y�@�S���ƭȪ��ɭԡA�~��F�쥭�šC�p�G�u��
��ۡA�Ҧp���P�T�A�hr��n��1�PF��n��1�A�]�Өt�Υu���@�ӦۥѫסC�bPT���u�W����
�@�I�W�A�o��۳��i�H�F�쥭�šA�o���u�W�C�I���ײv���i�Ѽ����{���w�C���u�@��
�������t�Φ۵M��[�����C
�۫����Y�b��ǻP�u�~�W�����n���@�����ΡA�K�O�X�����c����s�C�o�@��s���H
�̴��ѤF�㦳�S���ʽ�B�A�X��S���γ~���\�h���ݡC�o�譱���z�ץD�n�O�Q�ΤT�ع�
���k�Х߰_�Ӫ��G�]1�^�H�A�����G��I�k���ݡA��b��L��U��s��i�����I���F
�b1863�~�A�^���µẸ�w�]Sheffield�^��������]H C�DSorby�^�M�w��Lù�˳�
�]Charlottenburg�^�����y���]Martens�^�ХߤF�o�ؤ�k�A�D�n�O�ΨӬ�s�K�A���A
�o�Ӥ�k�S���ܤj����i�C�o�Ӥ�k�M���a���ܤF���ݻP�X�������鵲�c�C�]2�^����
�k�C�����Ī����ݧN�o�A��ɶ��M�ūץ[�H���q�C�����A���ܡA�Ҧp�ѲG�A�ܦ��T�A�ɡA
�ūת������ܸg�A�Φ��@�q�ɶ��������y�C�b�o�譱�A�i�H�|�X�|�����i�]Roozeboom�^
����N�����z�ת���s�]1900�~�^�M����J�]Heycock�^�P�������]Neville�^�����笰
�ҡC�]3�^X�g�u��k�C�o�Ӥ�k�O�Ҥ̡]Laue�^�P���Ԯ���h���l�Хߪ��A�����ܤF�T
��]���ר䬰�Q���B���ݩΦX���^����l���c�A�ö}�P�F�@���l��s���s���C
�����t����²�檺���ťi�H�ή���J�M����������ȻP�ɪ���s���Ҩӻ����C�»�
�u���uAE�]��6�^�q�G�A�̾���A�»ɪu���uBE�q�G�A�̾���C�b���IE�A�ȡB�ɨⴹ��
�P�ɥX�{�A�]�Ӿ��T�O�b���ܪ��ūפU�i�檺�C�b�o�ئX���̡A�ȥe40�H�A�ɥe60�H�A
�䵲�c�O���W�h���A�]�ӦW�s�u�����X���v�C
�p�G�T��H�G��@�˥i�H���ܨ�զ������A�ڭ̱N�o�ۡu�M���v�Ρu�T����v�A�P
������o�h���{�H�C�|�����i�����ΦN�������z�סA�ĩ��A�o�Dz{�H�C�b���ܩT���骺
�ϸ̡A�T�骺���צ��u�����I�����F�@�ӷ��C���B�H�����I�o�W���ūסC�b�o�̡A���
�T�A�ۤ@���q��L�T�A�۵����X�ӡA�ӧΦ��@�ئb���c�W���������X����������C��7
�O�����K�ҡ]�Ҥ֩�6�H�^�V�X�����|�����i�Ϫ��{�N�Φ��C�o�ӹϥi�H�����{�w�d��
�åB���F�W�٪��U�ؤƦX���P�T����A�Ʀܻ����F�����O�T�骺�U�ئX���b�T�w���ū�
�U���ܤơC�o�ت��۹����U�ڭ̱����զ������B�ūո`�P���z�ʽ褧�������Y�A�H��
�K�M���u�^���v�����G�C
��~�Ө�X�F�\�h�㦳�U�دS���ʽ�B�A�X�U�إγ~���s�X���A�S�O�O�K���X���C
�ѩM���ت��ϥΪ��X���p�����A�ѻs�y�Z���ϥΪ��K�X���A���t���ֶq����B�̡B���B
�뵥���ݡC�o�Ǫ��ݸg�L�A�������B�z����A�i���K����w�שΰ����W�j�Ψ㦳��L
�ݭn���ʽ�C�o�Ǫ�~�Ӫ��o�i���O�إߦb�W�z�z�P���窺��¦���W���C�H�U�|�X�X
�ӳo�˪��X�����Ҥl�G
�N3�H����[�b�示�A�W�[�j�צӤ���֩��@�C�p�G�ϥ�36�H���쪺�ܡA�ѩ�ҧt
�q�C�A���ȫY�ƱN�ܱo�ܷL�p�A�o�ئX���i�Ω�ܦh�γ~�A�٬��u����v�Ρu�]��
�]invar�^�X���v�C�ʯ�ϺҤƪ�í�w�A�[�ֳ\������A�ҳy�����X����ܻG�k�C���
���b������y�W�ܭ��n�A�S�O�O�t���ֳ\���̿��C���]��ϺҤƪ���[í�w�A�p�G
���������ܦh�h�y�����X�����ܡA���������A�h�@�ǡA�̫�N�s���t��12�H���u����
���v�C��o�ئX���������[�u�A�i�Ϩ���w�A��o�������ܿi�ʡA�`�ΥH��y�H�۾���
����C���l�q�j�A���֩T����̪����ʩʡA�]�ӫO�����ת���į�ܯ�O�A�é��w��
�ܡC����P�W���ۦP���i�ΥH��y������C
�b�D�K�X���̡A�T���X���S�O����A�]�S�O����λ��ȡC1909�~���k�A���թi
�]Wilm�^���H�}�l���o�ئX���i��{�u����s�C��ӥD�n�O�ѩ��Ťu�~�ݭn�軴��
�j�����ݡA�o�@��s�S���i�@�B���o�i�C�T�X���̦��@�ئW�s�u�w�T�v�A�t��4�H�A��0�D
5�H�M��O�D5�H�A��E95�H���T�C���ɶ��ҵw�ƫ�A�w�T���j�ץi�P�n���ۤ�C�٦��\
�h�O���T�X���P��L���ݪ��X���A�U�㦳�S�����ʽ�C
���O�DzĤ@�w�߬O��q�u����z�A�ĤG�w�߬O�i�Ϊ���q�U�ӷU�֡C�b��o���[��
�X�j���Ψ��ӫ��P�t�z�W���ɭԡA�N���H�{���A�t�z������q���_�a�q�L������Ƭ�
���Ӯ��O�F�A�P�ɡA�i�Ϊ�����S�]�Ůt��֦Ӥ��_�a��ְ_�ӡC��O���Ǫ��z�Ǯa�K
�Q��b�������N�Ӧt�z�����x�W���@���i�Ϊ���q�i�ೣ�n��Ʀ����A�������G��O��
���Ū����褤�A�H��N�û����i��A�������ܤƤF�C���o�ӵ��إߦb�X�ӥ��g��
�������]�W�C�]1�^�����w�ھڦ������[��G�o�X�����סA�b�j��W�٨S���˲M����
�s�x���������P�˦��ġF�]2�^�����w���P�t�z�O�t�ߪ���t�A�S����q�i�H�i�h�F�]3�^
�����w��Ӥ��l�ѩ۸I���A�t�פ��_�a���ܡA�ڭ̤���l�ܥ��̡A�⥦�̤����ֳt
�P�C�t�����C
���J�����Q�����@�ӷ��p���ͪ��Χ��]�A�����L�����Pı�A�i�H���ܨC�Ӥ��l����
�ʡA�t�d�z����W�@���L�������ưʪ��A������䦳��Ӹ˺����骺�ж��C���ֳt��
�l�ѥ���k�B�ʮɡA�p���ߨ�}���A���C�t���l�ӮɡA�L�ߨ������C��O�ֳt���l�E��
�b�k�ǡA�C�t���l�E���b���ǡC�k�Ǹ̪�����v���ܼ��A���Ǹ̪�����v���ܧN�C�o�ˡA
���F�����Ӥ��l����O�N�i�H���j������q���s�����_�ӡC
�b�Q�E�@���ҤF�Ѫ��۵M�ɪ����p�U�A�b�ڭ̥u��βέp����k�ӳB�z���l���ɭԡA
��q�Ӵ�����z��O�������C�H�̥ͬ��P���ʻݭn����q�������q�n�H���_�a�U�ӷU�֡A
�Ӽ��O�ǤW���I�ܪ��L�{�]���C�C�����t�z�̪��ͩR���M�I�C���ӷs���ѡA�o�ӵ�
�רs���b�h�j�{�פW�o��ק���ҹ�A�ڭ̱N�b�᭱���@�����A�[�z�C�b�o�̡A�ڭ�
���ӫ��X�A�����l���t���ӳ��J�����Ъi�����ҩw�ߤ��t���ɭԡA�i�F��̤j�ȡX�X
�Y��q���Ӵ��F��̤j���סX�X�����O�DZ���N�F��F�A�ӳo�ؤ��t�����v�o�O�@�ӳ�
�j�ȡC�o�ˡA�N����O�ǦP���v�ת��w���w�ߤΪ���B�ʽ��pô�_�ӤF�C
�����R
���ا�ѩM�a�ϧO�}�Ӫ��Dzάݪk�A�g�L��Ӥ��@���A�H���٬O�o�ˬ۫H�A�����Q
���P���y�o��o�جݪk���}�F�C�L�̥μƾǤ�k�P�[���k�ҩ��A�q�L����T�ߪ�����
�w�ߦb��ӤӶ��t���@�˾A�ΡC
�i�O�n�̫��ҩ��Ѧa�P�@�A�����ݭn�Ѧa�b�B�ʤ譱�O�������A�ӥB�ٻݭn�ҩ���
�a�b���c�W�P�զ������W�]�O�������A�ٻݭn�ҩ��c���a�W���骺�ߨ��ƾǤ����A�b��
���B��P�P���P�����褤�]�@�˪��s�b�C�o�n���O�@�ӵL�k�ѨM�����D�C�i�O�b�Q�E�@
�������o���F�@�ӸѨM����k�C
���y�w�g�ҩ�����q�L�W��ҧΦ����m����a�A�O�ѩ�ե����R�����z�W���²��
���������t�G�C1802�~�U�Դ��y�o�{�Ӷ������гQ�\�h�t�u�ҺI�_�F1814�~�����N�O
�]Joseph Fraunhofer�^���s�o�{�o�Ƿt�u�A�åΦh�ӸW��W�[���Ъ��ⴲ�סA�J�Ӧa
�N�t�u����m�yø�U�ӡC�t�@�譱�A1752�~�A���������]Melvil�^�����[���A���ݩ�
�Q�������K�ҳy�������СA�b�·t���I���W�e�{�S�����m����u�F1823�~�A�����E����
���]John Herschel�^��h�S�@�����ܳo���нu�i�H�Ψ�������ݪ��s�b�C�o��ij�ް_
�H�̹���нu��m�i���[���A�å[�H�yø�P�O���C
1849�~�A�����s�F���������q�����ҥͪ����СA�o�{�b������⤧���A�������
�u�A��b�����N�O�٬�D������t�u��m�W�C�����o�{������q�L�q���ɡAD�u�K���
���`���t�A�Y�N�@�Ӭ��������]���������ͳs����ЦӵL�t�u�^�q�L�q���A�hD�u�S�|
�X�{�C���컡�G�u�i���A�q���������O�o��D�u���A���YD�u�q�Ǫ������ӨӡA�q�����N
�[�H�l���C�v
�����N�O�нu���z�צn�H�����O�Ѵ����J���]George GabrielStokes�A1819��1903
�~�^�b�C�������t���[�H�ĩ����A�i�O�ѩ�L�S���������A�L�èS���N�L�����Ѽs�x��
�ǡC���������t����l���P�ۤv���ѵM���ʦX�窺�~�ӯ�q�A�����u�n��ൣ���H��
�_�a�����M�����۵M�\�ʶg���@�P���@�t�C�p�R���A�K��ϥ����������@�ˡC�Ӷ��~��
���]����l�]���w��l���q������������g�X���S�����u����q�A�u�n�o�ǥ��u������
�g���P�]����l�����ʶg���@�P�C�o�ˮg�Ӫ������w�ʤ֤F�㦳���دS�����ʶg������
�]�Y�Y�@��m�^�A���G�Ӷ����Ф��K���ͤ@���t�u�C
1855�~�A����H�����S�]David Alter�^�y�z�F�B�M��L���骺���СC1855��1863
�~���A���͡]von Bunsen�^�bù����]Roscoe�^���X�@�U�A�i��F�@�t�C������Ӭ�s
�����ƾǧ@�ΡA1859�~�A�L�P���N�ҡ]Kirchhoff�^�X�@�ХߤF�̦������Ф��R����
�T��k�A��O�ƾǤ����A�ɺޥu���L�q�A�]�i�ѥ��̪������ˬd�X�ӡC䣻P䧨�ӷs��
���N�O�γo�Ӥ�k�o�{���C
���ͻP���N�Ҧb�ƥ������D������窺���p�U�A���o�s����Ъ��ռ��ۦǥ��A�q
�L�t�����Q���s����K�A���G�A�ݨ�F�����N�O��D�нu�C�L�̤S��Y��b���ͷѮ�O
�����s�i��F�o�ӹ���A���@���b�Ӷ����Ф��䤣�쪺�t�u�C�L���_�w�Ӷ����j��
���ǡA���S���Y�A�Ϊ̬O�t�q�Ӥ֡A�[���C
�o�˶}�l��������оǡA�g�L�������]Huggins�^�B��ˡ]Jan��ssen�^�P���J�C
�]Lockyer�^���H���V�O�A���F�ܤj���o�i�C1878�~�A���J�C�b�Ӷ���y�h�����Ъ���
�ⳡ���ݨ��@���t�u�A�M�a�W���Ф�����w���u�����ŦX�C�L�M�����J���]Frankland�^
�@�P�w���A�Ӷ��̦��@�ӥi�H�����o�ز{�H�������F�L�̨ç�o�Ӥ����R�W����C1895
�~�A�ԩi�ɦb�@�ص����\�m�̵o�{�F�o�Ӥ����C
1842�~�A�h���ǡ]Doppler�^���X�A���@�Ӫi���P�[���̧@�۹�B�ʮɡA���[����
���i���W�v�K�|�o�ͧ��ܡC�p�G�i���V�[��̹G��ɡA�C�����F���[��̪��i�ƥ��w�W
�h�A���G�O�n�Υ����W�v�ܰ��C�Ϥ��A�i�����[��̦ӥh�ɡA�n�Υ����W�v���C�C�b��
����L�����ɡA�T���n���Ѱ��ӧC�A�N�R�������F�o���ܤơC�p�G�@���P�V�a�y�ӨӡA
����нu���V����@�ݲ��ʡA�p�G���a�y�ӥh�A�h�V����@�ݲ��ʡC�o�ئh���Ǯ�����
�M�ܤp�A�o�i�H�q�סA�g�L�������ΥH��\�h�H��s�A�ϧڭ̹���P�B�ʼW���F���֪�
�ѡA�b����٨ϧڭ̹��L�{�H�W���F���֪��ѡC
�P�ɥ��P��g���㦳�ۦP�����z�ʽ�A�]�o��R���ҩ��C1800�~�A�·G�E���˺�
�]William Herschel�^��h���X�A�N�ūp��b�Ӷ����Ф��N�i�H�ݥX�A�b�i��������
�����~�A�����������C�L�ᤣ�[�A�Q�S���]Ritter�^�o�{�i����������H�~�����g�u�A
�i�ϵv�Ļ��ܶ¡C1777�~�A�˰ǡ]Scheele�^�N�o�{�F�o����v�@�ΡC1830��1840�~���A
�������]Melloni�^�ҩ��ݤ�������g���M���@�ˡA���Ϯg�B��g�����B�z�A���ʽ�C
���\�h���z�Ǯa�A�S�O�O���N�ҡB�B�M���]Tyndall�^�P�j�����E���S�U�S�]Balfour
Stewart�^��o�g�P�l����رj�ת�������z�A�X�j���Ψ����g�C�L�̵o�{�A�@�ӯ�
�l���@����g������A�����ɤ]��o�g�@���i������g�C���p�U���S�]Prevost�^�b��
�洫�z�ס]1792�~�^�����X�A�@�����鳣��g���q�A�u�O�b���ŮɡA��ҧl�����q�굥
��ҵo�g���q�C
���J�����q�z�פW�ҩ���g�復�ҷӮg�����I�[�@�����O�A�o���O���M����L�p�A
����~�Ӥw�ι����k�[�H�ҹ�C1875�~�A�ڦ��Q�]Bartoli�^���X�o�����O���s�b��
�ڭ̷Q���@�ӥR����g���Ŷ��A�i�H���z�פW���������T���@�ΡC1884�~�A�i��������
�����骺�`��g���䵴��ūת��|����ӼW�[�A��H��aT4�C������]Stefan�^�b1879�~
�N�w�g�̸g��o�{�F�o�өw�ߡC�o�ӵ��G�ܦ��ΡA��������g�z�ܦ��ΡA�ӥB�i�H
�Q�γo�ӵ��G�A�q�L�[��ҩ�X������Ӵ��q���l���ūסA�ƦܤӶ��M���P�������ūסC
�ūW�[�ɡA�����`��g�ӳo�Ӥ覡�W�[�A�ӥB�ҵo�g��q���̤j�ȡA�]�V����u���i
������V���ʡC
�̫�A�@�Ӥ��������P�нu���W�v�������T�w���Y�A���M��G�Q�@���~�b���z�ǤW
��X�L���n�A�b�Q�E�@���ɴN�w�}�l�ް_�H�̪��`�N�C1885�~�A�ں��q�]Balmer�^
���X�B�������i�����и̪��|���u�A�i�Τ@�Ӹg�礽���ӥN���C��ӫ��������X�A�o��
�����٥i���F���~�нu���W�v�H�άP���нu�M�����ɤ�å��нu���W�v�A�]���A�o�ǥi
�ೣ�O�B�������нu�C�Ѧ��A�L�_�w�P���M��ä������B�����s�b�C
�q�i
�W�����L�A�k�ԲĪ��\�h�q�ǹ���u�@���k�\��L��q����ε��t�誺���n�ʪ���
��z�ѡC���q�y���@�ζV�L�Ŷ��Ϻϰw����Φb�����p���t�@�q���W���ͷP���q�y�ɡA
�ڭ̭n��N�����Q�����@�إ��g�������u�W�Z�@�Ρv�A�n��N�����Q���Ŷ��̦��@�ض�
�F���������١C�k�ԲĪ��ǤF�ĤG�طQ�k�C�L���Q�b�u�q�����ơv�̦��@�ǤO�u�Τ@��
���I��C�L�ƦܷQ���������}�ӷ���A�i�H�b�Ŷ��̦ۥѦ�i�C
���J�����]1831-1879�~�^��k�ԲĪ��Q�k�g���ƾǤ����C�L���X�k�ԲĹq������
�����ܧY�۷���q�y�C�J�M�q�y���ͺϳ��A�ϤO�P�q�y����A�ӥB�ϳ������ܤS���q
�ʤO�A��M�ϤO�P�q�O���ۤ������Y�C�]���A���q�����ƪ����ܦb���t���褤�A�|����
���ɡA�����@���q�Ϫi�Ӧ�i�A�q�O�P�ϤO�h�b�e�i���i�}���W�ۤ�����C
���J�����ҵo�{���L����{�������A�o�تi���t�ץu�H���誺�q�P�Ϫ��ʽ�Ӥ��P
�]�o�]�O�ܦ۵M���^�A�ӳo�ӳt�ץi����
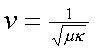 �����g�N�����誺�Ͼɲv�A�e�N�����q�`�Ʃιq�e�v�C
�ѩ��ӹq�������O�Pk���Ϥ�A��ӺϷ������O�P�g���Ϥ�A�ҥH�γo��ؤO��
�W�w���q�P�Ϫ���쥲�tk�P�g�C�ӥ����쪺�R�q�ȻP�q�ϭȤ���A�Ҧp�q�q�����A
���t�g�Pk�����n�C�ҥH�u�n�q�L��������ӳo�˪����A�K�i���w�q�Ϫi���t��v��
�ƭȡC
���J�����M�X�쪫�z�Ǯa�o�{�A�o�˴��w��v���ƭȬ��C��3��1010
���̡A�M�����t�ۦP�C��O���J�����_�w���O�q�ϲ{�H�A���F�@�إH�ӴN�i�H��
�����i�M�q�Ϫi�A�L�ݦA�r�y�n�X�إH�ӤF�C��ӥ��i�P�q�Ϫi�A�i�����M���P�ӫo�O
�P�����C
���O�ڭ̫�˹�ݤH�̤ƶO�F����h�ߦ�Ӭ�s���u�ʩT��H�өO�H�ڭ̨s������
��q�Ϫi�ݧ@�O�u��T��v�̪�����i�O�٬O���ӫ��N�q�٤����ժ��q�P�ϨӸ������O�H
���J�������o�{�A�Ĥ@���V�@�H���X�F�o�����D�C�i�O�L�o�[�j�F�H�̹��ǥ��H�Ӧs
�b���H�ߡC�ܩ���A�H�ӬJ��ǥ��A�]�����q���@�ΡC
���J��������s���G�b�^��ߨ�o��ӻ{�A���b�j���W�h�S���o�����o���`�N�C��
1887�~�A�����]Heinrich Hertz�^�~�ηP����W���q��ҵo�ͪ������q�y�A�b�Ŷ�����
�������q�i�A�ӥB�ι����k�ҩ��q�i�㦳�\�h�P���i�ۦP���ʽ�C�p�G�u�����H�ӡA
���̭��N�����F�u�L�u�q�i�v�A�ӳo�Ǫi�����O�b�Ů�̶Ǽ����C�o�@�o�{�D�n�����k
�\����J�����P�������u�@�C
���J�����n�D���z�Ǯa�����`�N���t������A�H���o�O�a�q�t�Τ��̭��n�������C
�ܩ���A�q�y����q�O�b���褤�q�L���A�ӹq�y�ۤv���L�O�o�د�q�Ӵ����������u�A
�o�����u���D�n�\�άO�ɯ�q�u�ۦ��i��Ӵ������|�e�i�C�b�ܨ��t�ܤƪ���y�q���A
�p�b�P���骺�q�᪺�q�y�ΰ{�q�q�᪺�q�y���A��q��i�J����A�q�y��V�N���ܤF�C
�]���A�u���ɽu���p�w�����֥i�H���Ħa�a�q�A�q���]�N��bí���q�y�����p�U���o
�h�C
���J�����z�ת��D�n�x���O�����q���������ժ������A�ܤ֤����k�ԲĪ��q��
����ҫ������۲�����l�q���������ժ������C���J�������ᤣ�[�A��l�q�����[���N
���F�����n�����D�A�ڭ̲{�b�N�����[�H�z�C���O�ڭ̶��o�����}���D�A�h�@�@�I�D
�~���ԭz�C
�ƾǧ@��
�ܦ��H�ӡA�ƾǧ@�Ϊ���]�P����K�����r�ת��D���A�ް_���y�ܦh���`�N�C1777
�~�A�ŵ����]C�DF Wenzel�^�i��F�T�w�����q�A�Q�q�L�[��ƾ��ܤƪ��t�רӦ��p��
�������ݪ��ƾǿ˦X�O�C�L�o�{�ƾǤ������ܤƲv�P�������@�סA�Y�վ������Ľ�q
����ҡA�������ܡ]Berthollet�^�]�W�߱o��o�ӵ��G�C
1850�~�A�·G�̡]Wilbelmy�^��s�F���}�[�Įɪ��u�ϱۡv�A�Y���}���l���Ѧ���
��²�檺���ۿ}�M�k�ۿ}���L�{�C�L�o�{�����}�G���@�צb�����i��L�{����֪��ɭԡA
�ܤƲv�K�P�ɶ����X��żƦ���ҦӴ�֡C�o�N�O���b�����������Ѫ����l�ƻP���ɦs
�b�����l�Ʀ���ҡX�X���w���}���l�����Ѥ����ۤz�A�o�ص��G�O�ܦ۵M���C���ޤ���
�ɭԡA�u�n�o�����Y���Y�@�ƾ��ܤƦ��ġA�ڭ̫K�i���_���l�O��Ӧa�b�_�@�ΡA��
�o���ܤƫK�٬�����l�����C
�t�@�譱�A�p�G��Ӥ��l���۰_�@�Ρ]�����l�����^�A�ܤƲv��M�M�w����l�I��
���W�v�A�ӳo�W�v�S�P��ذ_�@�Ϊ����l���@�שΦ��Ľ�q�����n����ҡC�p�G���l��
�@�۵��A�h�����n�N����@�ת�����C
�p�G�����O�i�f���A����ؤƦX��AB�PCD���ۧ@�ΦӦ�AD�PCB�ɡA��G�ئP�ɤ]��
�ۧ@�ΡA�Ӧ^��AB�PCD�F���ۤϪ��ܤƥH�P���ܤƲv�i��ɡA�Y��AB��CD����AD��CB�ɡA
�������Ū��A�C
�o�ذʺA���Ū��[���O�·G�ˡ]A�DW�DWilliamson�^�b1850�~�������մ��X���C
1864�~�A�j�w����]Guldberg�^�P�ˮ�]Waage�^��ƾǧ@�Ϊ���q�w�ߥ[�H��������
�z�F�ǧQ�S�]Jellet�^�b1873�~�A�S�S���N�ҡ]Van�zt Hoff�^�b1877�~�S���s�o�{�F
�o�өw�ߡC�o�өw�ߤ����p�W�ҭz�A�i�Ѥ��l�B�ʲz�ױ��X�A�]�i�ھڼ��O�ǭ�z�q�H
�G��t����q���Y���ɥX�ӡC���b�\�h�ƾǤ������o�����W���ҩ��C
�W�����L�A���}���ϱۦb�������b���ɶi��o�ܧ֡A�_�h�i��o���C�C�����èS��
���ܤơA���n�H�u�P�i�����A�ۤv�ä��ѥ[�����C�o�@�{�H�b1812�~���������N�ҵo
�{�C�L�o�{�b�H���ķ��G���A�����i�ܤƬ�����}�C�����`�N��`��ϾJ�]�T�b�Ů�
��ơC�h����ǡ]Dobereiner�^��o�{�`�������i�ϲB��G��ƦX�C1838�~�A�w�Ԧ���
�]Cagniard de Latour�^�P�I���]Schwann�^�U���ۿѦa�o�{�}�ҥH��o�æӦ��s��P
�G��ƺҡA�O�ѩ�@�طL�ͪ����@�ΡA�f���d������X�o�ûP�`���ҫP�����L��������
�ۦ��ʡC�f���d����o�ا@�Υs���u�ʤơv�A���P���ƾǤ������վ��㦳�u�ʤƯ�O�v�C
�L���X�b�ͪ��餤�Ѵ��q����B�Ӫ��G�ĩΦ�ӥͦ����L�ƺؤƦX���A�i��O��������
�ƾ���������һs�����C1878�~�A�w���]Kuhne�^��o�Ǧ����ʤƾ��s���u���v�λï��C
1862�~�A���S���]Berthelot�^�P�t�N�Ǵ��]Pean de St Gilles�^�o�{�A�p�����l
��ұN�A��L�ĻP���V�X�A�g�L�X�P������A�A��L�ĴN�������ѦӦ��A�J�P�L�ġA��
�ƪ��t�O����C�p�G�q�s��P�Ķ}�l�A�h�ƾ��ܤƴ¤Ϥ�V�i��A�̫ᥭ�Ůɪ���
�ҬO�ۦP���C�o�Ǥ����ܺC�A���p���q�Ħb���A�h�X�I�����Y�i�F��P�˪����šC�o��
�ĴN���F�@�ضʤƾ��A�ӥB�i�H�ݥX�A�ʤƾ����\�Φb��P�i��Ӥ�V������@�Ӥ�V
���ƾǤ����C�q�Y�طN�q�W���A�����@�ΡA�n�H�Ƽ���������Ұ_���@�Τ@�ˡC1887�~�A
���֧Q�Q���]Arrhenius�^�o�{�������ʤƧ@�λP��ɹq�v�����C
����]���P�˪��{�H�C1880�~�A�f�J���]Dixon�^�o�{�p�G�B��G��ܰ���A�o��
�خ���N�����z���Ӧ�����C1794�~�A�I�ǩi�]Fulhame�^�ҤH�w���[���o�Ӳ{�H�C
1902�~�A���J�]BreretonBaker�^���X�A�p�ƦX�i��o�ܺC�åB�Φ��F���A�N�S���z��
�{�H�C���i���S�ԡ]Armstrong�^���ܡA�����ۨ��ҧΦ������L��º�A�S���ʤƧ@�ΡC
�ڧڭ̩Ҫ��A�٦��@�ǮɭԡA�º骺�ƾǪ���]�O���_�@�Ϊ��A���G�����������V�X��
�b���A�~��P�i�ܤơC�����ʤƾ��Ρ��b�ͪ���ǤW�����n�ʱN�b�H��X�����ԭz�C
�Q�E�@���̫�X�~�o�{�F�X�ӷs���k�ʤ����C1895�~�A�ĤT�N�p�Q��h�]third
Lord Rayleigh�^�`�N��A�q�Ů�o�Ӫ����q��ƦX���o�Ӫ��A�K�n�j�@�ǡA�]��
�ɤޥL�M�ԩi�ɵo�{�F�@�شk��A�R�W����C��۵o�{���٦���]�Ѭ�241���^�B�ߡB
���P�I�A�o�O�|�~���q�Ů�̵o�{�����ӷs�����C��{�b�Ω�K�����R��q�O�A��P��
�Ω�s�i�O�i�O�A���]������㦳��z�ʡA��Ω�O��C�M�O���ѵM��@�D�q�[���j�M
���ꪺ�Y�Ǥg�a�̳v�X�����A�L�h�ΨӥR��W����y�C�o�Ǥ����b���o�C�C�ҩP
�������Φ���l�����s���@�ڡA�Ӧb�H��n�ԭz�������Q����l�Ǽƪ��̤]����A����
�a��C�����y���H��ӹ���l�q�P�P����Ҷi�檺��s�ϱo�o�Ǯ���b�z�פW��H�e
��[���n�C
���G�z��
����b�����Ψ�L�G�餤�i�H���ѡA�o�O�H�Ҽ������{�H�C���DzG��A�p�s��P���A
�������ҳ��i���۲V�X�A�Ӧ��DzG��p�o�P���A�@�I�]����V�X�C�T��p�}�i�b����
�ۥѷ��ѡA���ݴN�����ѡF�Ů�P����������Ȥֳ\���ѩ���A�Ӯ��P�B��Į�h�j
�q���ѡC
���z�ܤƥi�P���ѦP�ɵo�͡C���G���e�n�i���M�����ۥ[���e�n�p�A�ӥB�i
��l���M����{�H�C�\�h�����Q���ѩ���ɲ��ͭP�N�����A�i�O�]���ּ��Q���p���
�T���Ѯɵo�X���ӡC�����P�P���]�`�o���C
�o�Ǥ����A�g�L�\�h�ƾǮa��s�C�L�̻{�Ѩ�o�ؤ������ʽ�ܽ����A�䤤���V�X
�P�ƦX��ر��ΡA���L�A���̪��������_���ܡ]�P��L�ƦX�������@�w��Ҥ��P�^����
�䶡�s�b���@�ǯS�����Y�C���b�Q�E�@���H�e�S���H�N���G�{�H���@�S�����D�C
�������t�Φa��s���Ѫ��誺�X�����H�O��p�̩i�]ThomasCraham�A1805��1869
�~�^�C�L�������X��������A�ڭ̦b�e���w�g���L�F�C��p�̩i�o�{�A����A�p�\�h
�Q���A���ѩ���ɡA�`��ۥѦa��L�����A�i�H����֦a�q���G���@�����X����t�@��
���C�������@�����Φ����骺����A���ѫ��X������w�C�C��p�̩i�ٲĤ@�����鬰��
����A�ĤG��������C�_��H�����饲�w�O�������A����Ӥ~���D�\�h�L�����p���Ư~�A
�Ʀܪ��ݦp�����A�g�L�S���B�z�A�]�i�H�e���骬�A�C
��S�q�����o���H�Υߨ��H���ӨӪ����G�q�ѩʽ誺��s�A�w�g�ԭz�L�F�C
1833�~�A�k�Բī��X�A�Ϥ@�w�q�q�q�L�q�ѲG�ɡA�`�O���@�w�q�����l�b�q���W�R�X�C
�p�G�ڭ̧�q�y�ݧ@�O�a���l���B�ʦӶǻ����A�o�N�N���ۨC�@�ӭ�l���ۦP�����l��
�w�a�ۦP�˪��q���A�o�˳�����l�ұa���q���A�N���F�۵M�����ιq��l�C
1859�~�A�Ʀ��ҡ]Hittorf�^�b�o�Ӱ��D�W�S�e�i�F�@�B�C�L���q�y�q�L��Ӥ���
���q���A���G��ӹq�������G�N�{�פ����a�}���_�ӡC�Ʀ��ҬݥX�A�Q�γo�Өƹ�
�N�i�H�ι����k�ⲧ�����l�B�ʪ��t�ץ[�H����A�]�o��t���j�����l���q������
�h���h���q�ѽ�C�o�˴N�i�H���w��ز������l���t�פ�C
1879�~�A�캸�ҬI�]Kohlrausch�^�o���A�@�Ӵ��q�q�ѲG�q�����n��k�C�ѩ�
�@�ΡA���y�q�O����ϥΪ��A���캸�ҬI�o�J�A�F�o�ӧx���C�L���ΤF��y�q�M�j���n
���������q���A�Ӵ�֨I�����������K�סC�L���ιq�y�p�A�ӥι��y�q���������q��
���ӧ@���ܾ��C�b�o���קK�F���Ƨ@�Τ���A�L�o�{�q�ѲG�]�A�q�کi�w�ߡA�Y�q�y�P
�q�ʤO����ҡC�]���̤p���q�ʤO�]�i�H�Ϲq�ѽ褤���ͬ������q�y�F���F�b�q������
���~�A�]�S�����ƪ��ϧ@�ΡC�ҥH���l���w�i�H�ۥѥ洫�A���J�ҭE���һ������ˡC
�캸�ҬI�N�o�˴��w�F�q�ѽ誺�Ǿɲv�A�åB���X�ѩ�q�y���ϦV���l�y�Ҷǰe�A
�Ǿɲv�@�w�i�H�ΨӴ��q�ϦV���l�t�ת��`�M�C�A�[�W�Ʀ��Ҫ����w���l�t�פ���
�k�A�ڭ̴N�i�H�p��ӧO���l���t�פF�C�b�C���̦�1��S�q��t����פU�A�B�b����
�B�ʪ��t���C��0�D003���̡A�Ӥ����Q�������l���t�h�����C��0�D0006���̡C�B
���l���t�ȡA�g���v�]Oliver Lodge�^��h�b���礤�[�H�ҹ�C�L�Τ@�ع�B�F�Ӫ�
���ܾ��������ۦ�A�ϲB���l�q�L�䤤�A�M��[�H�l��C�����Q���l���ƭȡA�h������
�@�̩��ҹ�]���ѧ@���[��F���̦b�ۦ��Q�������B�ʡ^�A�q�I�����Φ����]�i�H�o��
�ҹ�C�o�Ǥ�k�H��S�Ѱ��ˡ]Masson�^�B�������]Steele�^�B���������]Maclnnes�^
����s�̥[�H��i�C
�������z�Ǯa�S�S-�N�ҹ�G���t�~�@�جݪk�C�ڭ̦��w���D�A�g�L�ӭM����
���J�Ӫ��ӭM�����A�i�H���ͤ@�����O�A�Ӫ��Ǯa�إ��]Pfeffer�^�ΤH�u�����A�Y�b
�L�V�����W�ΤƾǤ�k�y���I���ӻs���������A�q�L�o�غ��z���C�S�S-�N�ҫ��X�A
�إ������q�����A���z���M��L�]�������Y�ܶH���骺���O�A�Y�P�e�n���Ϥ�A���H��
��ūצӼW�[�C�b���G���ຯ�z���������A���Ψ�L�����i�H�i��i�f�����z���{�H��
�ڭ̥i�H�]�Q�㦳���z�ʪ��ӭM�N�O�@�Ӳz�Q�������T���A�]���A�S�S-�N�ҥi�H���
�O�Ǫ����z���Ψ췻�G�W�h�A�q�Ӷ}�P�F�@�ӷs����s���C�L�N���G�����z���M��L
���z�ʽ�p���T�I�B�T�����pô�_�ӡA�o�ˡA�q�L���q���T�I�]�o�O�@������e������
�u�@�^�A�N�i�H��X���z���C�L�q�z�פW�ҩ��}���G�����z��������ȥ��P�P�@�ת���
�����O�ۦP�A�M��L�S�ι����ҩ��F�o�ӵ��G�C�ڭ̨ä�����ǤH�ҳ]�Q�����˦]��
�N�o�X�����F������O�㦳�ۦP����]�A�η��Ѫ�����O���ۮ��骬�A�C���O�Ǫ���
�z�ä��A�ξ�����D�A���������pô���q���������Y�A���o���A�γo���pô���ʽ�C
���z���]�\�H���骺���O�@�ˡA�O�ѩ���l���I���Ӳ��ͪ��F�]�\�O�ѩ�P������
�����ƾǿ˦X�O�ΤƾǤƦX�Ӳ��ͪ��C���ޥ����ʽ��ˡA�u�n���s�b�A���N���w�A�X
���O�ǭ�z�A�b�}���G���A�p�S�S���N�ҩ��ҩ����A���N���w���`����w�ߡC�i�O����
��]���w�A�ܤ֤��O���O�ǩү�T�w���C
1887�~�A���H���֧Q�Q���ҩ����z���P���G���q�ѩʦ����D�ڭ̳����D�A�q�ѽ�
�����z�����`���j�A�Ҧp��ƹ[�Υ����������G���Q�������G�A�����O���P���l�@�ת�
�}���G�����O���⭿�C���֧Q�Q���o�{�A�o�دS�j�����O�����P�q�Ѫ��ɹq�צ����A��
�B�P�ƾǪ����ʩʡA�p�����b�}�o�æ��ܬ��s�몺�L�{�����ʤƯ�O�]�����Y�C�L����
�O�o�����O�����q�ѽ褤���l�������ѡA�]���A�|�Ҩӻ��A�b��ƹ[���G���A���M��
�Y�z���ʪ�KCI���l�s�b�A�P�ɤ]���[���l�P�����l�U�a�ۥ��q���P�t�q���A�������G
�ɹq�P�ƾǬ��ʩʪ��ӷ��C���G�V�H�A���Ѫ��Q�V�h�A�췻�G�H�췥�ɡA�G���u��
K�����l�MCI�����l�C���H�{���o������l�������}�A�O�M�����ƦX�b�@�_���C
�캸�ҬI�B�S�S���N�ҡB���֧Q�Q�����u�@���F���z�ƾǪ��e�j���W�h�j�H���_�I�C
�b�o�y�j�H�̡A���O�ǻP�q�ǵ��X�_�ӡA�ϲz�ת����Ѥ��_�a�W�i�A�åB�U�ӷU�s�x�a
������Ω�u�~�C�����p���A�ڭ̤]���n�ѰO��Ӧ��@�ǰ��j�����z�Ǯa��s�F�q�b��
�餤���ǾɡA�ئ��F�{�N��Ǥ��̦��S�x�ʪ��@�Ӥ���A�ӥL�̪����l�[���o�O���G�z
�����L�̪��C
�q���窺�[�I�ӬݡA�������w���z���O�ܧx�����A���O�A���ꪺ�������]Morse�^
�P�h�S���]Whitney�^�A�H�έ^�ꪺ���J�ܡ]Berke��ley�^�B��P���S�ܡ]E�DG�DJ�D
Hartley�^�A�o����b1901�~�M1906��1916�~���A�ﰪ�@�ת����G�������z���i��F��
�����w�C�������P�L���P�ƩҥΪ����w��k�W�P�إ�����k�ۦP�A�u�O�b�Ӹ`�W�j
����i�C���J�ܻP���S�ܨèS���[������y�J�b�b���z���p�Ǹ̳y�������O�A�ӬO��
���G����v���W�������O�A���췻������B�ʪ���V�Q�����X�h�C�L�̧�ұo�����G�M
�S�E�w�E�˺�����{���]��232���^�[�H����F�N���}�P����}�Ө��A�o�{�P�U�C����
�̲ŦX�G
�����g�N�����誺�Ͼɲv�A�e�N�����q�`�Ʃιq�e�v�C
�ѩ��ӹq�������O�Pk���Ϥ�A��ӺϷ������O�P�g���Ϥ�A�ҥH�γo��ؤO��
�W�w���q�P�Ϫ���쥲�tk�P�g�C�ӥ����쪺�R�q�ȻP�q�ϭȤ���A�Ҧp�q�q�����A
���t�g�Pk�����n�C�ҥH�u�n�q�L��������ӳo�˪����A�K�i���w�q�Ϫi���t��v��
�ƭȡC
���J�����M�X�쪫�z�Ǯa�o�{�A�o�˴��w��v���ƭȬ��C��3��1010
���̡A�M�����t�ۦP�C��O���J�����_�w���O�q�ϲ{�H�A���F�@�إH�ӴN�i�H��
�����i�M�q�Ϫi�A�L�ݦA�r�y�n�X�إH�ӤF�C��ӥ��i�P�q�Ϫi�A�i�����M���P�ӫo�O
�P�����C
���O�ڭ̫�˹�ݤH�̤ƶO�F����h�ߦ�Ӭ�s���u�ʩT��H�өO�H�ڭ̨s������
��q�Ϫi�ݧ@�O�u��T��v�̪�����i�O�٬O���ӫ��N�q�٤����ժ��q�P�ϨӸ������O�H
���J�������o�{�A�Ĥ@���V�@�H���X�F�o�����D�C�i�O�L�o�[�j�F�H�̹��ǥ��H�Ӧs
�b���H�ߡC�ܩ���A�H�ӬJ��ǥ��A�]�����q���@�ΡC
���J��������s���G�b�^��ߨ�o��ӻ{�A���b�j���W�h�S���o�����o���`�N�C��
1887�~�A�����]Heinrich Hertz�^�~�ηP����W���q��ҵo�ͪ������q�y�A�b�Ŷ�����
�������q�i�A�ӥB�ι����k�ҩ��q�i�㦳�\�h�P���i�ۦP���ʽ�C�p�G�u�����H�ӡA
���̭��N�����F�u�L�u�q�i�v�A�ӳo�Ǫi�����O�b�Ů�̶Ǽ����C�o�@�o�{�D�n�����k
�\����J�����P�������u�@�C
���J�����n�D���z�Ǯa�����`�N���t������A�H���o�O�a�q�t�Τ��̭��n�������C
�ܩ���A�q�y����q�O�b���褤�q�L���A�ӹq�y�ۤv���L�O�o�د�q�Ӵ����������u�A
�o�����u���D�n�\�άO�ɯ�q�u�ۦ��i��Ӵ������|�e�i�C�b�ܨ��t�ܤƪ���y�q���A
�p�b�P���骺�q�᪺�q�y�ΰ{�q�q�᪺�q�y���A��q��i�J����A�q�y��V�N���ܤF�C
�]���A�u���ɽu���p�w�����֥i�H���Ħa�a�q�A�q���]�N��bí���q�y�����p�U���o
�h�C
���J�����z�ת��D�n�x���O�����q���������ժ������A�ܤ֤����k�ԲĪ��q��
����ҫ������۲�����l�q���������ժ������C���J�������ᤣ�[�A��l�q�����[���N
���F�����n�����D�A�ڭ̲{�b�N�����[�H�z�C���O�ڭ̶��o�����}���D�A�h�@�@�I�D
�~���ԭz�C
�ƾǧ@��
�ܦ��H�ӡA�ƾǧ@�Ϊ���]�P����K�����r�ת��D���A�ް_���y�ܦh���`�N�C1777
�~�A�ŵ����]C�DF Wenzel�^�i��F�T�w�����q�A�Q�q�L�[��ƾ��ܤƪ��t�רӦ��p��
�������ݪ��ƾǿ˦X�O�C�L�o�{�ƾǤ������ܤƲv�P�������@�סA�Y�վ������Ľ�q
����ҡA�������ܡ]Berthollet�^�]�W�߱o��o�ӵ��G�C
1850�~�A�·G�̡]Wilbelmy�^��s�F���}�[�Įɪ��u�ϱۡv�A�Y���}���l���Ѧ���
��²�檺���ۿ}�M�k�ۿ}���L�{�C�L�o�{�����}�G���@�צb�����i��L�{����֪��ɭԡA
�ܤƲv�K�P�ɶ����X��żƦ���ҦӴ�֡C�o�N�O���b�����������Ѫ����l�ƻP���ɦs
�b�����l�Ʀ���ҡX�X���w���}���l�����Ѥ����ۤz�A�o�ص��G�O�ܦ۵M���C���ޤ���
�ɭԡA�u�n�o�����Y���Y�@�ƾ��ܤƦ��ġA�ڭ̫K�i���_���l�O��Ӧa�b�_�@�ΡA��
�o���ܤƫK�٬�����l�����C
�t�@�譱�A�p�G��Ӥ��l���۰_�@�Ρ]�����l�����^�A�ܤƲv��M�M�w����l�I��
���W�v�A�ӳo�W�v�S�P��ذ_�@�Ϊ����l���@�שΦ��Ľ�q�����n����ҡC�p�G���l��
�@�۵��A�h�����n�N����@�ת�����C
�p�G�����O�i�f���A����ؤƦX��AB�PCD���ۧ@�ΦӦ�AD�PCB�ɡA��G�ئP�ɤ]��
�ۧ@�ΡA�Ӧ^��AB�PCD�F���ۤϪ��ܤƥH�P���ܤƲv�i��ɡA�Y��AB��CD����AD��CB�ɡA
�������Ū��A�C
�o�ذʺA���Ū��[���O�·G�ˡ]A�DW�DWilliamson�^�b1850�~�������մ��X���C
1864�~�A�j�w����]Guldberg�^�P�ˮ�]Waage�^��ƾǧ@�Ϊ���q�w�ߥ[�H��������
�z�F�ǧQ�S�]Jellet�^�b1873�~�A�S�S���N�ҡ]Van�zt Hoff�^�b1877�~�S���s�o�{�F
�o�өw�ߡC�o�өw�ߤ����p�W�ҭz�A�i�Ѥ��l�B�ʲz�ױ��X�A�]�i�ھڼ��O�ǭ�z�q�H
�G��t����q���Y���ɥX�ӡC���b�\�h�ƾǤ������o�����W���ҩ��C
�W�����L�A���}���ϱۦb�������b���ɶi��o�ܧ֡A�_�h�i��o���C�C�����èS��
���ܤơA���n�H�u�P�i�����A�ۤv�ä��ѥ[�����C�o�@�{�H�b1812�~���������N�ҵo
�{�C�L�o�{�b�H���ķ��G���A�����i�ܤƬ�����}�C�����`�N��`��ϾJ�]�T�b�Ů�
��ơC�h����ǡ]Dobereiner�^��o�{�`�������i�ϲB��G��ƦX�C1838�~�A�w�Ԧ���
�]Cagniard de Latour�^�P�I���]Schwann�^�U���ۿѦa�o�{�}�ҥH��o�æӦ��s��P
�G��ƺҡA�O�ѩ�@�طL�ͪ����@�ΡA�f���d������X�o�ûP�`���ҫP�����L��������
�ۦ��ʡC�f���d����o�ا@�Υs���u�ʤơv�A���P���ƾǤ������վ��㦳�u�ʤƯ�O�v�C
�L���X�b�ͪ��餤�Ѵ��q����B�Ӫ��G�ĩΦ�ӥͦ����L�ƺؤƦX���A�i��O��������
�ƾ���������һs�����C1878�~�A�w���]Kuhne�^��o�Ǧ����ʤƾ��s���u���v�λï��C
1862�~�A���S���]Berthelot�^�P�t�N�Ǵ��]Pean de St Gilles�^�o�{�A�p�����l
��ұN�A��L�ĻP���V�X�A�g�L�X�P������A�A��L�ĴN�������ѦӦ��A�J�P�L�ġA��
�ƪ��t�O����C�p�G�q�s��P�Ķ}�l�A�h�ƾ��ܤƴ¤Ϥ�V�i��A�̫ᥭ�Ůɪ���
�ҬO�ۦP���C�o�Ǥ����ܺC�A���p���q�Ħb���A�h�X�I�����Y�i�F��P�˪����šC�o��
�ĴN���F�@�ضʤƾ��A�ӥB�i�H�ݥX�A�ʤƾ����\�Φb��P�i��Ӥ�V������@�Ӥ�V
���ƾǤ����C�q�Y�طN�q�W���A�����@�ΡA�n�H�Ƽ���������Ұ_���@�Τ@�ˡC1887�~�A
���֧Q�Q���]Arrhenius�^�o�{�������ʤƧ@�λP��ɹq�v�����C
����]���P�˪��{�H�C1880�~�A�f�J���]Dixon�^�o�{�p�G�B��G��ܰ���A�o��
�خ���N�����z���Ӧ�����C1794�~�A�I�ǩi�]Fulhame�^�ҤH�w���[���o�Ӳ{�H�C
1902�~�A���J�]BreretonBaker�^���X�A�p�ƦX�i��o�ܺC�åB�Φ��F���A�N�S���z��
�{�H�C���i���S�ԡ]Armstrong�^���ܡA�����ۨ��ҧΦ������L��º�A�S���ʤƧ@�ΡC
�ڧڭ̩Ҫ��A�٦��@�ǮɭԡA�º骺�ƾǪ���]�O���_�@�Ϊ��A���G�����������V�X��
�b���A�~��P�i�ܤơC�����ʤƾ��Ρ��b�ͪ���ǤW�����n�ʱN�b�H��X�����ԭz�C
�Q�E�@���̫�X�~�o�{�F�X�ӷs���k�ʤ����C1895�~�A�ĤT�N�p�Q��h�]third
Lord Rayleigh�^�`�N��A�q�Ů�o�Ӫ����q��ƦX���o�Ӫ��A�K�n�j�@�ǡA�]��
�ɤޥL�M�ԩi�ɵo�{�F�@�شk��A�R�W����C��۵o�{���٦���]�Ѭ�241���^�B�ߡB
���P�I�A�o�O�|�~���q�Ů�̵o�{�����ӷs�����C��{�b�Ω�K�����R��q�O�A��P��
�Ω�s�i�O�i�O�A���]������㦳��z�ʡA��Ω�O��C�M�O���ѵM��@�D�q�[���j�M
���ꪺ�Y�Ǥg�a�̳v�X�����A�L�h�ΨӥR��W����y�C�o�Ǥ����b���o�C�C�ҩP
�������Φ���l�����s���@�ڡA�Ӧb�H��n�ԭz�������Q����l�Ǽƪ��̤]����A����
�a��C�����y���H��ӹ���l�q�P�P����Ҷi�檺��s�ϱo�o�Ǯ���b�z�פW��H�e
��[���n�C
���G�z��
����b�����Ψ�L�G�餤�i�H���ѡA�o�O�H�Ҽ������{�H�C���DzG��A�p�s��P���A
�������ҳ��i���۲V�X�A�Ӧ��DzG��p�o�P���A�@�I�]����V�X�C�T��p�}�i�b����
�ۥѷ��ѡA���ݴN�����ѡF�Ů�P����������Ȥֳ\���ѩ���A�Ӯ��P�B��Į�h�j
�q���ѡC
���z�ܤƥi�P���ѦP�ɵo�͡C���G���e�n�i���M�����ۥ[���e�n�p�A�ӥB�i
��l���M����{�H�C�\�h�����Q���ѩ���ɲ��ͭP�N�����A�i�O�]���ּ��Q���p���
�T���Ѯɵo�X���ӡC�����P�P���]�`�o���C
�o�Ǥ����A�g�L�\�h�ƾǮa��s�C�L�̻{�Ѩ�o�ؤ������ʽ�ܽ����A�䤤���V�X
�P�ƦX��ر��ΡA���L�A���̪��������_���ܡ]�P��L�ƦX�������@�w��Ҥ��P�^����
�䶡�s�b���@�ǯS�����Y�C���b�Q�E�@���H�e�S���H�N���G�{�H���@�S�����D�C
�������t�Φa��s���Ѫ��誺�X�����H�O��p�̩i�]ThomasCraham�A1805��1869
�~�^�C�L�������X��������A�ڭ̦b�e���w�g���L�F�C��p�̩i�o�{�A����A�p�\�h
�Q���A���ѩ���ɡA�`��ۥѦa��L�����A�i�H����֦a�q���G���@�����X����t�@��
���C�������@�����Φ����骺����A���ѫ��X������w�C�C��p�̩i�ٲĤ@�����鬰��
����A�ĤG��������C�_��H�����饲�w�O�������A����Ӥ~���D�\�h�L�����p���Ư~�A
�Ʀܪ��ݦp�����A�g�L�S���B�z�A�]�i�H�e���骬�A�C
��S�q�����o���H�Υߨ��H���ӨӪ����G�q�ѩʽ誺��s�A�w�g�ԭz�L�F�C
1833�~�A�k�Բī��X�A�Ϥ@�w�q�q�q�L�q�ѲG�ɡA�`�O���@�w�q�����l�b�q���W�R�X�C
�p�G�ڭ̧�q�y�ݧ@�O�a���l���B�ʦӶǻ����A�o�N�N���ۨC�@�ӭ�l���ۦP�����l��
�w�a�ۦP�˪��q���A�o�˳�����l�ұa���q���A�N���F�۵M�����ιq��l�C
1859�~�A�Ʀ��ҡ]Hittorf�^�b�o�Ӱ��D�W�S�e�i�F�@�B�C�L���q�y�q�L��Ӥ���
���q���A���G��ӹq�������G�N�{�פ����a�}���_�ӡC�Ʀ��ҬݥX�A�Q�γo�Өƹ�
�N�i�H�ι����k�ⲧ�����l�B�ʪ��t�ץ[�H����A�]�o��t���j�����l���q������
�h���h���q�ѽ�C�o�˴N�i�H���w��ز������l���t�פ�C
1879�~�A�캸�ҬI�]Kohlrausch�^�o���A�@�Ӵ��q�q�ѲG�q�����n��k�C�ѩ�
�@�ΡA���y�q�O����ϥΪ��A���캸�ҬI�o�J�A�F�o�ӧx���C�L���ΤF��y�q�M�j���n
���������q���A�Ӵ�֨I�����������K�סC�L���ιq�y�p�A�ӥι��y�q���������q��
���ӧ@���ܾ��C�b�o���קK�F���Ƨ@�Τ���A�L�o�{�q�ѲG�]�A�q�کi�w�ߡA�Y�q�y�P
�q�ʤO����ҡC�]���̤p���q�ʤO�]�i�H�Ϲq�ѽ褤���ͬ������q�y�F���F�b�q������
���~�A�]�S�����ƪ��ϧ@�ΡC�ҥH���l���w�i�H�ۥѥ洫�A���J�ҭE���һ������ˡC
�캸�ҬI�N�o�˴��w�F�q�ѽ誺�Ǿɲv�A�åB���X�ѩ�q�y���ϦV���l�y�Ҷǰe�A
�Ǿɲv�@�w�i�H�ΨӴ��q�ϦV���l�t�ת��`�M�C�A�[�W�Ʀ��Ҫ����w���l�t�פ���
�k�A�ڭ̴N�i�H�p��ӧO���l���t�פF�C�b�C���̦�1��S�q��t����פU�A�B�b����
�B�ʪ��t���C��0�D003���̡A�Ӥ����Q�������l���t�h�����C��0�D0006���̡C�B
���l���t�ȡA�g���v�]Oliver Lodge�^��h�b���礤�[�H�ҹ�C�L�Τ@�ع�B�F�Ӫ�
���ܾ��������ۦ�A�ϲB���l�q�L�䤤�A�M��[�H�l��C�����Q���l���ƭȡA�h������
�@�̩��ҹ�]���ѧ@���[��F���̦b�ۦ��Q�������B�ʡ^�A�q�I�����Φ����]�i�H�o��
�ҹ�C�o�Ǥ�k�H��S�Ѱ��ˡ]Masson�^�B�������]Steele�^�B���������]Maclnnes�^
����s�̥[�H��i�C
�������z�Ǯa�S�S-�N�ҹ�G���t�~�@�جݪk�C�ڭ̦��w���D�A�g�L�ӭM����
���J�Ӫ��ӭM�����A�i�H���ͤ@�����O�A�Ӫ��Ǯa�إ��]Pfeffer�^�ΤH�u�����A�Y�b
�L�V�����W�ΤƾǤ�k�y���I���ӻs���������A�q�L�o�غ��z���C�S�S-�N�ҫ��X�A
�إ������q�����A���z���M��L�]�������Y�ܶH���骺���O�A�Y�P�e�n���Ϥ�A���H��
��ūצӼW�[�C�b���G���ຯ�z���������A���Ψ�L�����i�H�i��i�f�����z���{�H��
�ڭ̥i�H�]�Q�㦳���z�ʪ��ӭM�N�O�@�Ӳz�Q�������T���A�]���A�S�S-�N�ҥi�H���
�O�Ǫ����z���Ψ췻�G�W�h�A�q�Ӷ}�P�F�@�ӷs����s���C�L�N���G�����z���M��L
���z�ʽ�p���T�I�B�T�����pô�_�ӡA�o�ˡA�q�L���q���T�I�]�o�O�@������e������
�u�@�^�A�N�i�H��X���z���C�L�q�z�פW�ҩ��}���G�����z��������ȥ��P�P�@�ת���
�����O�ۦP�A�M��L�S�ι����ҩ��F�o�ӵ��G�C�ڭ̨ä�����ǤH�ҳ]�Q�����˦]��
�N�o�X�����F������O�㦳�ۦP����]�A�η��Ѫ�����O���ۮ��骬�A�C���O�Ǫ���
�z�ä��A�ξ�����D�A���������pô���q���������Y�A���o���A�γo���pô���ʽ�C
���z���]�\�H���骺���O�@�ˡA�O�ѩ���l���I���Ӳ��ͪ��F�]�\�O�ѩ�P������
�����ƾǿ˦X�O�ΤƾǤƦX�Ӳ��ͪ��C���ޥ����ʽ��ˡA�u�n���s�b�A���N���w�A�X
���O�ǭ�z�A�b�}���G���A�p�S�S���N�ҩ��ҩ����A���N���w���`����w�ߡC�i�O����
��]���w�A�ܤ֤��O���O�ǩү�T�w���C
1887�~�A���H���֧Q�Q���ҩ����z���P���G���q�ѩʦ����D�ڭ̳����D�A�q�ѽ�
�����z�����`���j�A�Ҧp��ƹ[�Υ����������G���Q�������G�A�����O���P���l�@�ת�
�}���G�����O���⭿�C���֧Q�Q���o�{�A�o�دS�j�����O�����P�q�Ѫ��ɹq�צ����A��
�B�P�ƾǪ����ʩʡA�p�����b�}�o�æ��ܬ��s�몺�L�{�����ʤƯ�O�]�����Y�C�L����
�O�o�����O�����q�ѽ褤���l�������ѡA�]���A�|�Ҩӻ��A�b��ƹ[���G���A���M��
�Y�z���ʪ�KCI���l�s�b�A�P�ɤ]���[���l�P�����l�U�a�ۥ��q���P�t�q���A�������G
�ɹq�P�ƾǬ��ʩʪ��ӷ��C���G�V�H�A���Ѫ��Q�V�h�A�췻�G�H�췥�ɡA�G���u��
K�����l�MCI�����l�C���H�{���o������l�������}�A�O�M�����ƦX�b�@�_���C
�캸�ҬI�B�S�S���N�ҡB���֧Q�Q�����u�@���F���z�ƾǪ��e�j���W�h�j�H���_�I�C
�b�o�y�j�H�̡A���O�ǻP�q�ǵ��X�_�ӡA�ϲz�ת����Ѥ��_�a�W�i�A�åB�U�ӷU�s�x�a
������Ω�u�~�C�����p���A�ڭ̤]���n�ѰO��Ӧ��@�ǰ��j�����z�Ǯa��s�F�q�b��
�餤���ǾɡA�ئ��F�{�N��Ǥ��̦��S�x�ʪ��@�Ӥ���A�ӥL�̪����l�[���o�O���G�z
�����L�̪��C
�q���窺�[�I�ӬݡA�������w���z���O�ܧx�����A���O�A���ꪺ�������]Morse�^
�P�h�S���]Whitney�^�A�H�έ^�ꪺ���J�ܡ]Berke��ley�^�B��P���S�ܡ]E�DG�DJ�D
Hartley�^�A�o����b1901�~�M1906��1916�~���A�ﰪ�@�ת����G�������z���i��F��
�����w�C�������P�L���P�ƩҥΪ����w��k�W�P�إ�����k�ۦP�A�u�O�b�Ӹ`�W�j
����i�C���J�ܻP���S�ܨèS���[������y�J�b�b���z���p�Ǹ̳y�������O�A�ӬO��
���G����v���W�������O�A���췻������B�ʪ���V�Q�����X�h�C�L�̧�ұo�����G�M
�S�E�w�E�˺�����{���]��232���^�[�H����F�N���}�P����}�Ө��A�o�{�P�U�C����
�̲ŦX�G
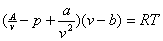 �����S�˺��w�]ostwald�^���q�@�Ϊ��ƾǩw�ߡ]245���^���Ω���֧Q�Q���ҷQ
�H���q�ѽ誺���ѡA���@�ӵ}�Ʃw�ߡG
�����S�˺��w�]ostwald�^���q�@�Ϊ��ƾǩw�ߡ]245���^���Ω���֧Q�Q���ҷQ
�H���q�ѽ誺���ѡA���@�ӵ}�Ʃw�ߡG
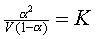 �����\�N���q���סAV�N�����G���e�n�AK�O�`�ơC�o�Ӥ�{�����z���q�ѽ観�ġA
�p�������Ѫ��ĩM�Q�A�o�ɤW���ܬ�
�����\�N���q���סAV�N�����G���e�n�AK�O�`�ơC�o�Ӥ�{�����z���q�ѽ観�ġA
�p�������Ѫ��ĩM�Q�A�o�ɤW���ܬ�
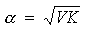 ������������Ѫ��q�ѽ�L�ġA�o�@���ѡA���ܪ��ɶ������q���z�פ��ର�H
�������@�ӻ�ê�C
�o�ӧx�����̪�s�j��W�J�A�C1923��1927�~���A�w���]Debxe�^�B�溸
�]Huckel�^�P���Į�]onsager�^���X�A�ѩ����l�����@�ΤO�A���l�P��Φ��@�ز���
�����l�j��C���l�B�ʮɡA�����b�e���ذ_�@�ӷs���j��A�Ө�I�᪺�j������C�o�@
�@�ΧΦ��@�ت��ת��q�즲�A�ϥ����B�ʡA�P��@�ת�����ڦ���ҦӴ�֡C�o�˴N��
�X�@�Ӭ۷���������{���C�p�N���l���i��l�X�@�֭p�J�A�o�Ӥ�{���P����ӱo��
���Y�A�Y�@�P�ɹq�ת����Y�A�j�P�ŦX�A�N�O��j�q�ѽ�@���G�ӻ��]�O�p���C
���֧Q�Q�{���j�q�ѽ�u���������ѡA�ӳ̪�s�o�����O�����q���C�ܩ�@��
�G�̬۹�q���ת���֡A���O�ѩ����l�t�ת��ܽw���t�G�C��X�g�u���R�A������l�N
�O�b�T�A�����餺�A�]�O�������}�A�H��A�]���H���X�o�˪��ݪk�]��384�A427��8��
���^�C
------------------
�@�@���߾ǭb ������z
������������Ѫ��q�ѽ�L�ġA�o�@���ѡA���ܪ��ɶ������q���z�פ��ର�H
�������@�ӻ�ê�C
�o�ӧx�����̪�s�j��W�J�A�C1923��1927�~���A�w���]Debxe�^�B�溸
�]Huckel�^�P���Į�]onsager�^���X�A�ѩ����l�����@�ΤO�A���l�P��Φ��@�ز���
�����l�j��C���l�B�ʮɡA�����b�e���ذ_�@�ӷs���j��A�Ө�I�᪺�j������C�o�@
�@�ΧΦ��@�ت��ת��q�즲�A�ϥ����B�ʡA�P��@�ת�����ڦ���ҦӴ�֡C�o�˴N��
�X�@�Ӭ۷���������{���C�p�N���l���i��l�X�@�֭p�J�A�o�Ӥ�{���P����ӱo��
���Y�A�Y�@�P�ɹq�ת����Y�A�j�P�ŦX�A�N�O��j�q�ѽ�@���G�ӻ��]�O�p���C
���֧Q�Q�{���j�q�ѽ�u���������ѡA�ӳ̪�s�o�����O�����q���C�ܩ�@��
�G�̬۹�q���ת���֡A���O�ѩ����l�t�ת��ܽw���t�G�C��X�g�u���R�A������l�N
�O�b�T�A�����餺�A�]�O�������}�A�H��A�]���H���X�o�˪��ݪk�]��384�A427��8��
���^�C
------------------
�@�@���߾ǭb ������z
|
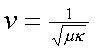 �����g�N�����誺�Ͼɲv�A�e�N�����q�`�Ʃιq�e�v�C
�ѩ��ӹq�������O�Pk���Ϥ�A��ӺϷ������O�P�g���Ϥ�A�ҥH�γo��ؤO��
�W�w���q�P�Ϫ���쥲�tk�P�g�C�ӥ����쪺�R�q�ȻP�q�ϭȤ���A�Ҧp�q�q�����A
���t�g�Pk�����n�C�ҥH�u�n�q�L��������ӳo�˪����A�K�i���w�q�Ϫi���t��v��
�ƭȡC
���J�����M�X�쪫�z�Ǯa�o�{�A�o�˴��w��v���ƭȬ��C��3��1010
���̡A�M�����t�ۦP�C��O���J�����_�w���O�q�ϲ{�H�A���F�@�إH�ӴN�i�H��
�����i�M�q�Ϫi�A�L�ݦA�r�y�n�X�إH�ӤF�C��ӥ��i�P�q�Ϫi�A�i�����M���P�ӫo�O
�P�����C
���O�ڭ̫�˹�ݤH�̤ƶO�F����h�ߦ�Ӭ�s���u�ʩT��H�өO�H�ڭ̨s������
��q�Ϫi�ݧ@�O�u��T��v�̪�����i�O�٬O���ӫ��N�q�٤����ժ��q�P�ϨӸ������O�H
���J�������o�{�A�Ĥ@���V�@�H���X�F�o�����D�C�i�O�L�o�[�j�F�H�̹��ǥ��H�Ӧs
�b���H�ߡC�ܩ���A�H�ӬJ��ǥ��A�]�����q���@�ΡC
���J��������s���G�b�^��ߨ�o��ӻ{�A���b�j���W�h�S���o�����o���`�N�C��
1887�~�A�����]Heinrich Hertz�^�~�ηP����W���q��ҵo�ͪ������q�y�A�b�Ŷ�����
�������q�i�A�ӥB�ι����k�ҩ��q�i�㦳�\�h�P���i�ۦP���ʽ�C�p�G�u�����H�ӡA
���̭��N�����F�u�L�u�q�i�v�A�ӳo�Ǫi�����O�b�Ů�̶Ǽ����C�o�@�o�{�D�n�����k
�\����J�����P�������u�@�C
���J�����n�D���z�Ǯa�����`�N���t������A�H���o�O�a�q�t�Τ��̭��n�������C
�ܩ���A�q�y����q�O�b���褤�q�L���A�ӹq�y�ۤv���L�O�o�د�q�Ӵ����������u�A
�o�����u���D�n�\�άO�ɯ�q�u�ۦ��i��Ӵ������|�e�i�C�b�ܨ��t�ܤƪ���y�q���A
�p�b�P���骺�q�᪺�q�y�ΰ{�q�q�᪺�q�y���A��q��i�J����A�q�y��V�N���ܤF�C
�]���A�u���ɽu���p�w�����֥i�H���Ħa�a�q�A�q���]�N��bí���q�y�����p�U���o
�h�C
���J�����z�ת��D�n�x���O�����q���������ժ������A�ܤ֤����k�ԲĪ��q��
����ҫ������۲�����l�q���������ժ������C���J�������ᤣ�[�A��l�q�����[���N
���F�����n�����D�A�ڭ̲{�b�N�����[�H�z�C���O�ڭ̶��o�����}���D�A�h�@�@�I�D
�~���ԭz�C
�ƾǧ@��
�ܦ��H�ӡA�ƾǧ@�Ϊ���]�P����K�����r�ת��D���A�ް_���y�ܦh���`�N�C1777
�~�A�ŵ����]C�DF Wenzel�^�i��F�T�w�����q�A�Q�q�L�[��ƾ��ܤƪ��t�רӦ��p��
�������ݪ��ƾǿ˦X�O�C�L�o�{�ƾǤ������ܤƲv�P�������@�סA�Y�վ������Ľ�q
����ҡA�������ܡ]Berthollet�^�]�W�߱o��o�ӵ��G�C
1850�~�A�·G�̡]Wilbelmy�^��s�F���}�[�Įɪ��u�ϱۡv�A�Y���}���l���Ѧ���
��²�檺���ۿ}�M�k�ۿ}���L�{�C�L�o�{�����}�G���@�צb�����i��L�{����֪��ɭԡA
�ܤƲv�K�P�ɶ����X��żƦ���ҦӴ�֡C�o�N�O���b�����������Ѫ����l�ƻP���ɦs
�b�����l�Ʀ���ҡX�X���w���}���l�����Ѥ����ۤz�A�o�ص��G�O�ܦ۵M���C���ޤ���
�ɭԡA�u�n�o�����Y���Y�@�ƾ��ܤƦ��ġA�ڭ̫K�i���_���l�O��Ӧa�b�_�@�ΡA��
�o���ܤƫK�٬�����l�����C
�t�@�譱�A�p�G��Ӥ��l���۰_�@�Ρ]�����l�����^�A�ܤƲv��M�M�w����l�I��
���W�v�A�ӳo�W�v�S�P��ذ_�@�Ϊ����l���@�שΦ��Ľ�q�����n����ҡC�p�G���l��
�@�۵��A�h�����n�N����@�ת�����C
�p�G�����O�i�f���A����ؤƦX��AB�PCD���ۧ@�ΦӦ�AD�PCB�ɡA��G�ئP�ɤ]��
�ۧ@�ΡA�Ӧ^��AB�PCD�F���ۤϪ��ܤƥH�P���ܤƲv�i��ɡA�Y��AB��CD����AD��CB�ɡA
�������Ū��A�C
�o�ذʺA���Ū��[���O�·G�ˡ]A�DW�DWilliamson�^�b1850�~�������մ��X���C
1864�~�A�j�w����]Guldberg�^�P�ˮ�]Waage�^��ƾǧ@�Ϊ���q�w�ߥ[�H��������
�z�F�ǧQ�S�]Jellet�^�b1873�~�A�S�S���N�ҡ]Van�zt Hoff�^�b1877�~�S���s�o�{�F
�o�өw�ߡC�o�өw�ߤ����p�W�ҭz�A�i�Ѥ��l�B�ʲz�ױ��X�A�]�i�ھڼ��O�ǭ�z�q�H
�G��t����q���Y���ɥX�ӡC���b�\�h�ƾǤ������o�����W���ҩ��C
�W�����L�A���}���ϱۦb�������b���ɶi��o�ܧ֡A�_�h�i��o���C�C�����èS��
���ܤơA���n�H�u�P�i�����A�ۤv�ä��ѥ[�����C�o�@�{�H�b1812�~���������N�ҵo
�{�C�L�o�{�b�H���ķ��G���A�����i�ܤƬ�����}�C�����`�N��`��ϾJ�]�T�b�Ů�
��ơC�h����ǡ]Dobereiner�^��o�{�`�������i�ϲB��G��ƦX�C1838�~�A�w�Ԧ���
�]Cagniard de Latour�^�P�I���]Schwann�^�U���ۿѦa�o�{�}�ҥH��o�æӦ��s��P
�G��ƺҡA�O�ѩ�@�طL�ͪ����@�ΡA�f���d������X�o�ûP�`���ҫP�����L��������
�ۦ��ʡC�f���d����o�ا@�Υs���u�ʤơv�A���P���ƾǤ������վ��㦳�u�ʤƯ�O�v�C
�L���X�b�ͪ��餤�Ѵ��q����B�Ӫ��G�ĩΦ�ӥͦ����L�ƺؤƦX���A�i��O��������
�ƾ���������һs�����C1878�~�A�w���]Kuhne�^��o�Ǧ����ʤƾ��s���u���v�λï��C
1862�~�A���S���]Berthelot�^�P�t�N�Ǵ��]Pean de St Gilles�^�o�{�A�p�����l
��ұN�A��L�ĻP���V�X�A�g�L�X�P������A�A��L�ĴN�������ѦӦ��A�J�P�L�ġA��
�ƪ��t�O����C�p�G�q�s��P�Ķ}�l�A�h�ƾ��ܤƴ¤Ϥ�V�i��A�̫ᥭ�Ůɪ���
�ҬO�ۦP���C�o�Ǥ����ܺC�A���p���q�Ħb���A�h�X�I�����Y�i�F��P�˪����šC�o��
�ĴN���F�@�ضʤƾ��A�ӥB�i�H�ݥX�A�ʤƾ����\�Φb��P�i��Ӥ�V������@�Ӥ�V
���ƾǤ����C�q�Y�طN�q�W���A�����@�ΡA�n�H�Ƽ���������Ұ_���@�Τ@�ˡC1887�~�A
���֧Q�Q���]Arrhenius�^�o�{�������ʤƧ@�λP��ɹq�v�����C
����]���P�˪��{�H�C1880�~�A�f�J���]Dixon�^�o�{�p�G�B��G��ܰ���A�o��
�خ���N�����z���Ӧ�����C1794�~�A�I�ǩi�]Fulhame�^�ҤH�w���[���o�Ӳ{�H�C
1902�~�A���J�]BreretonBaker�^���X�A�p�ƦX�i��o�ܺC�åB�Φ��F���A�N�S���z��
�{�H�C���i���S�ԡ]Armstrong�^���ܡA�����ۨ��ҧΦ������L��º�A�S���ʤƧ@�ΡC
�ڧڭ̩Ҫ��A�٦��@�ǮɭԡA�º骺�ƾǪ���]�O���_�@�Ϊ��A���G�����������V�X��
�b���A�~��P�i�ܤơC�����ʤƾ��Ρ��b�ͪ���ǤW�����n�ʱN�b�H��X�����ԭz�C
�Q�E�@���̫�X�~�o�{�F�X�ӷs���k�ʤ����C1895�~�A�ĤT�N�p�Q��h�]third
Lord Rayleigh�^�`�N��A�q�Ů�o�Ӫ����q��ƦX���o�Ӫ��A�K�n�j�@�ǡA�]��
�ɤޥL�M�ԩi�ɵo�{�F�@�شk��A�R�W����C��۵o�{���٦���]�Ѭ�241���^�B�ߡB
���P�I�A�o�O�|�~���q�Ů�̵o�{�����ӷs�����C��{�b�Ω�K�����R��q�O�A��P��
�Ω�s�i�O�i�O�A���]������㦳��z�ʡA��Ω�O��C�M�O���ѵM��@�D�q�[���j�M
���ꪺ�Y�Ǥg�a�̳v�X�����A�L�h�ΨӥR��W����y�C�o�Ǥ����b���o�C�C�ҩP
�������Φ���l�����s���@�ڡA�Ӧb�H��n�ԭz�������Q����l�Ǽƪ��̤]����A����
�a��C�����y���H��ӹ���l�q�P�P����Ҷi�檺��s�ϱo�o�Ǯ���b�z�פW��H�e
��[���n�C
���G�z��
����b�����Ψ�L�G�餤�i�H���ѡA�o�O�H�Ҽ������{�H�C���DzG��A�p�s��P���A
�������ҳ��i���۲V�X�A�Ӧ��DzG��p�o�P���A�@�I�]����V�X�C�T��p�}�i�b����
�ۥѷ��ѡA���ݴN�����ѡF�Ů�P����������Ȥֳ\���ѩ���A�Ӯ��P�B��Į�h�j
�q���ѡC
���z�ܤƥi�P���ѦP�ɵo�͡C���G���e�n�i���M�����ۥ[���e�n�p�A�ӥB�i
��l���M����{�H�C�\�h�����Q���ѩ���ɲ��ͭP�N�����A�i�O�]���ּ��Q���p���
�T���Ѯɵo�X���ӡC�����P�P���]�`�o���C
�o�Ǥ����A�g�L�\�h�ƾǮa��s�C�L�̻{�Ѩ�o�ؤ������ʽ�ܽ����A�䤤���V�X
�P�ƦX��ر��ΡA���L�A���̪��������_���ܡ]�P��L�ƦX�������@�w��Ҥ��P�^����
�䶡�s�b���@�ǯS�����Y�C���b�Q�E�@���H�e�S���H�N���G�{�H���@�S�����D�C
�������t�Φa��s���Ѫ��誺�X�����H�O��p�̩i�]ThomasCraham�A1805��1869
�~�^�C�L�������X��������A�ڭ̦b�e���w�g���L�F�C��p�̩i�o�{�A����A�p�\�h
�Q���A���ѩ���ɡA�`��ۥѦa��L�����A�i�H����֦a�q���G���@�����X����t�@��
���C�������@�����Φ����骺����A���ѫ��X������w�C�C��p�̩i�ٲĤ@�����鬰��
����A�ĤG��������C�_��H�����饲�w�O�������A����Ӥ~���D�\�h�L�����p���Ư~�A
�Ʀܪ��ݦp�����A�g�L�S���B�z�A�]�i�H�e���骬�A�C
��S�q�����o���H�Υߨ��H���ӨӪ����G�q�ѩʽ誺��s�A�w�g�ԭz�L�F�C
1833�~�A�k�Բī��X�A�Ϥ@�w�q�q�q�L�q�ѲG�ɡA�`�O���@�w�q�����l�b�q���W�R�X�C
�p�G�ڭ̧�q�y�ݧ@�O�a���l���B�ʦӶǻ����A�o�N�N���ۨC�@�ӭ�l���ۦP�����l��
�w�a�ۦP�˪��q���A�o�˳�����l�ұa���q���A�N���F�۵M�����ιq��l�C
1859�~�A�Ʀ��ҡ]Hittorf�^�b�o�Ӱ��D�W�S�e�i�F�@�B�C�L���q�y�q�L��Ӥ���
���q���A���G��ӹq�������G�N�{�פ����a�}���_�ӡC�Ʀ��ҬݥX�A�Q�γo�Өƹ�
�N�i�H�ι����k�ⲧ�����l�B�ʪ��t�ץ[�H����A�]�o��t���j�����l���q������
�h���h���q�ѽ�C�o�˴N�i�H���w��ز������l���t�פ�C
1879�~�A�캸�ҬI�]Kohlrausch�^�o���A�@�Ӵ��q�q�ѲG�q�����n��k�C�ѩ�
�@�ΡA���y�q�O����ϥΪ��A���캸�ҬI�o�J�A�F�o�ӧx���C�L���ΤF��y�q�M�j���n
���������q���A�Ӵ�֨I�����������K�סC�L���ιq�y�p�A�ӥι��y�q���������q��
���ӧ@���ܾ��C�b�o���קK�F���Ƨ@�Τ���A�L�o�{�q�ѲG�]�A�q�کi�w�ߡA�Y�q�y�P
�q�ʤO����ҡC�]���̤p���q�ʤO�]�i�H�Ϲq�ѽ褤���ͬ������q�y�F���F�b�q������
���~�A�]�S�����ƪ��ϧ@�ΡC�ҥH���l���w�i�H�ۥѥ洫�A���J�ҭE���һ������ˡC
�캸�ҬI�N�o�˴��w�F�q�ѽ誺�Ǿɲv�A�åB���X�ѩ�q�y���ϦV���l�y�Ҷǰe�A
�Ǿɲv�@�w�i�H�ΨӴ��q�ϦV���l�t�ת��`�M�C�A�[�W�Ʀ��Ҫ����w���l�t�פ���
�k�A�ڭ̴N�i�H�p��ӧO���l���t�פF�C�b�C���̦�1��S�q��t����פU�A�B�b����
�B�ʪ��t���C��0�D003���̡A�Ӥ����Q�������l���t�h�����C��0�D0006���̡C�B
���l���t�ȡA�g���v�]Oliver Lodge�^��h�b���礤�[�H�ҹ�C�L�Τ@�ع�B�F�Ӫ�
���ܾ��������ۦ�A�ϲB���l�q�L�䤤�A�M��[�H�l��C�����Q���l���ƭȡA�h������
�@�̩��ҹ�]���ѧ@���[��F���̦b�ۦ��Q�������B�ʡ^�A�q�I�����Φ����]�i�H�o��
�ҹ�C�o�Ǥ�k�H��S�Ѱ��ˡ]Masson�^�B�������]Steele�^�B���������]Maclnnes�^
����s�̥[�H��i�C
�������z�Ǯa�S�S-�N�ҹ�G���t�~�@�جݪk�C�ڭ̦��w���D�A�g�L�ӭM����
���J�Ӫ��ӭM�����A�i�H���ͤ@�����O�A�Ӫ��Ǯa�إ��]Pfeffer�^�ΤH�u�����A�Y�b
�L�V�����W�ΤƾǤ�k�y���I���ӻs���������A�q�L�o�غ��z���C�S�S-�N�ҫ��X�A
�إ������q�����A���z���M��L�]�������Y�ܶH���骺���O�A�Y�P�e�n���Ϥ�A���H��
��ūצӼW�[�C�b���G���ຯ�z���������A���Ψ�L�����i�H�i��i�f�����z���{�H��
�ڭ̥i�H�]�Q�㦳���z�ʪ��ӭM�N�O�@�Ӳz�Q�������T���A�]���A�S�S-�N�ҥi�H���
�O�Ǫ����z���Ψ췻�G�W�h�A�q�Ӷ}�P�F�@�ӷs����s���C�L�N���G�����z���M��L
���z�ʽ�p���T�I�B�T�����pô�_�ӡA�o�ˡA�q�L���q���T�I�]�o�O�@������e������
�u�@�^�A�N�i�H��X���z���C�L�q�z�פW�ҩ��}���G�����z��������ȥ��P�P�@�ת���
�����O�ۦP�A�M��L�S�ι����ҩ��F�o�ӵ��G�C�ڭ̨ä�����ǤH�ҳ]�Q�����˦]��
�N�o�X�����F������O�㦳�ۦP����]�A�η��Ѫ�����O���ۮ��骬�A�C���O�Ǫ���
�z�ä��A�ξ�����D�A���������pô���q���������Y�A���o���A�γo���pô���ʽ�C
���z���]�\�H���骺���O�@�ˡA�O�ѩ���l���I���Ӳ��ͪ��F�]�\�O�ѩ�P������
�����ƾǿ˦X�O�ΤƾǤƦX�Ӳ��ͪ��C���ޥ����ʽ��ˡA�u�n���s�b�A���N���w�A�X
���O�ǭ�z�A�b�}���G���A�p�S�S���N�ҩ��ҩ����A���N���w���`����w�ߡC�i�O����
��]���w�A�ܤ֤��O���O�ǩү�T�w���C
1887�~�A���H���֧Q�Q���ҩ����z���P���G���q�ѩʦ����D�ڭ̳����D�A�q�ѽ�
�����z�����`���j�A�Ҧp��ƹ[�Υ����������G���Q�������G�A�����O���P���l�@�ת�
�}���G�����O���⭿�C���֧Q�Q���o�{�A�o�دS�j�����O�����P�q�Ѫ��ɹq�צ����A��
�B�P�ƾǪ����ʩʡA�p�����b�}�o�æ��ܬ��s�몺�L�{�����ʤƯ�O�]�����Y�C�L����
�O�o�����O�����q�ѽ褤���l�������ѡA�]���A�|�Ҩӻ��A�b��ƹ[���G���A���M��
�Y�z���ʪ�KCI���l�s�b�A�P�ɤ]���[���l�P�����l�U�a�ۥ��q���P�t�q���A�������G
�ɹq�P�ƾǬ��ʩʪ��ӷ��C���G�V�H�A���Ѫ��Q�V�h�A�췻�G�H�췥�ɡA�G���u��
K�����l�MCI�����l�C���H�{���o������l�������}�A�O�M�����ƦX�b�@�_���C
�캸�ҬI�B�S�S���N�ҡB���֧Q�Q�����u�@���F���z�ƾǪ��e�j���W�h�j�H���_�I�C
�b�o�y�j�H�̡A���O�ǻP�q�ǵ��X�_�ӡA�ϲz�ת����Ѥ��_�a�W�i�A�åB�U�ӷU�s�x�a
������Ω�u�~�C�����p���A�ڭ̤]���n�ѰO��Ӧ��@�ǰ��j�����z�Ǯa��s�F�q�b��
�餤���ǾɡA�ئ��F�{�N��Ǥ��̦��S�x�ʪ��@�Ӥ���A�ӥL�̪����l�[���o�O���G�z
�����L�̪��C
�q���窺�[�I�ӬݡA�������w���z���O�ܧx�����A���O�A���ꪺ�������]Morse�^
�P�h�S���]Whitney�^�A�H�έ^�ꪺ���J�ܡ]Berke��ley�^�B��P���S�ܡ]E�DG�DJ�D
Hartley�^�A�o����b1901�~�M1906��1916�~���A�ﰪ�@�ת����G�������z���i��F��
�����w�C�������P�L���P�ƩҥΪ����w��k�W�P�إ�����k�ۦP�A�u�O�b�Ӹ`�W�j
����i�C���J�ܻP���S�ܨèS���[������y�J�b�b���z���p�Ǹ̳y�������O�A�ӬO��
���G����v���W�������O�A���췻������B�ʪ���V�Q�����X�h�C�L�̧�ұo�����G�M
�S�E�w�E�˺�����{���]��232���^�[�H����F�N���}�P����}�Ө��A�o�{�P�U�C����
�̲ŦX�G
�����g�N�����誺�Ͼɲv�A�e�N�����q�`�Ʃιq�e�v�C
�ѩ��ӹq�������O�Pk���Ϥ�A��ӺϷ������O�P�g���Ϥ�A�ҥH�γo��ؤO��
�W�w���q�P�Ϫ���쥲�tk�P�g�C�ӥ����쪺�R�q�ȻP�q�ϭȤ���A�Ҧp�q�q�����A
���t�g�Pk�����n�C�ҥH�u�n�q�L��������ӳo�˪����A�K�i���w�q�Ϫi���t��v��
�ƭȡC
���J�����M�X�쪫�z�Ǯa�o�{�A�o�˴��w��v���ƭȬ��C��3��1010
���̡A�M�����t�ۦP�C��O���J�����_�w���O�q�ϲ{�H�A���F�@�إH�ӴN�i�H��
�����i�M�q�Ϫi�A�L�ݦA�r�y�n�X�إH�ӤF�C��ӥ��i�P�q�Ϫi�A�i�����M���P�ӫo�O
�P�����C
���O�ڭ̫�˹�ݤH�̤ƶO�F����h�ߦ�Ӭ�s���u�ʩT��H�өO�H�ڭ̨s������
��q�Ϫi�ݧ@�O�u��T��v�̪�����i�O�٬O���ӫ��N�q�٤����ժ��q�P�ϨӸ������O�H
���J�������o�{�A�Ĥ@���V�@�H���X�F�o�����D�C�i�O�L�o�[�j�F�H�̹��ǥ��H�Ӧs
�b���H�ߡC�ܩ���A�H�ӬJ��ǥ��A�]�����q���@�ΡC
���J��������s���G�b�^��ߨ�o��ӻ{�A���b�j���W�h�S���o�����o���`�N�C��
1887�~�A�����]Heinrich Hertz�^�~�ηP����W���q��ҵo�ͪ������q�y�A�b�Ŷ�����
�������q�i�A�ӥB�ι����k�ҩ��q�i�㦳�\�h�P���i�ۦP���ʽ�C�p�G�u�����H�ӡA
���̭��N�����F�u�L�u�q�i�v�A�ӳo�Ǫi�����O�b�Ů�̶Ǽ����C�o�@�o�{�D�n�����k
�\����J�����P�������u�@�C
���J�����n�D���z�Ǯa�����`�N���t������A�H���o�O�a�q�t�Τ��̭��n�������C
�ܩ���A�q�y����q�O�b���褤�q�L���A�ӹq�y�ۤv���L�O�o�د�q�Ӵ����������u�A
�o�����u���D�n�\�άO�ɯ�q�u�ۦ��i��Ӵ������|�e�i�C�b�ܨ��t�ܤƪ���y�q���A
�p�b�P���骺�q�᪺�q�y�ΰ{�q�q�᪺�q�y���A��q��i�J����A�q�y��V�N���ܤF�C
�]���A�u���ɽu���p�w�����֥i�H���Ħa�a�q�A�q���]�N��bí���q�y�����p�U���o
�h�C
���J�����z�ת��D�n�x���O�����q���������ժ������A�ܤ֤����k�ԲĪ��q��
����ҫ������۲�����l�q���������ժ������C���J�������ᤣ�[�A��l�q�����[���N
���F�����n�����D�A�ڭ̲{�b�N�����[�H�z�C���O�ڭ̶��o�����}���D�A�h�@�@�I�D
�~���ԭz�C
�ƾǧ@��
�ܦ��H�ӡA�ƾǧ@�Ϊ���]�P����K�����r�ת��D���A�ް_���y�ܦh���`�N�C1777
�~�A�ŵ����]C�DF Wenzel�^�i��F�T�w�����q�A�Q�q�L�[��ƾ��ܤƪ��t�רӦ��p��
�������ݪ��ƾǿ˦X�O�C�L�o�{�ƾǤ������ܤƲv�P�������@�סA�Y�վ������Ľ�q
����ҡA�������ܡ]Berthollet�^�]�W�߱o��o�ӵ��G�C
1850�~�A�·G�̡]Wilbelmy�^��s�F���}�[�Įɪ��u�ϱۡv�A�Y���}���l���Ѧ���
��²�檺���ۿ}�M�k�ۿ}���L�{�C�L�o�{�����}�G���@�צb�����i��L�{����֪��ɭԡA
�ܤƲv�K�P�ɶ����X��żƦ���ҦӴ�֡C�o�N�O���b�����������Ѫ����l�ƻP���ɦs
�b�����l�Ʀ���ҡX�X���w���}���l�����Ѥ����ۤz�A�o�ص��G�O�ܦ۵M���C���ޤ���
�ɭԡA�u�n�o�����Y���Y�@�ƾ��ܤƦ��ġA�ڭ̫K�i���_���l�O��Ӧa�b�_�@�ΡA��
�o���ܤƫK�٬�����l�����C
�t�@�譱�A�p�G��Ӥ��l���۰_�@�Ρ]�����l�����^�A�ܤƲv��M�M�w����l�I��
���W�v�A�ӳo�W�v�S�P��ذ_�@�Ϊ����l���@�שΦ��Ľ�q�����n����ҡC�p�G���l��
�@�۵��A�h�����n�N����@�ת�����C
�p�G�����O�i�f���A����ؤƦX��AB�PCD���ۧ@�ΦӦ�AD�PCB�ɡA��G�ئP�ɤ]��
�ۧ@�ΡA�Ӧ^��AB�PCD�F���ۤϪ��ܤƥH�P���ܤƲv�i��ɡA�Y��AB��CD����AD��CB�ɡA
�������Ū��A�C
�o�ذʺA���Ū��[���O�·G�ˡ]A�DW�DWilliamson�^�b1850�~�������մ��X���C
1864�~�A�j�w����]Guldberg�^�P�ˮ�]Waage�^��ƾǧ@�Ϊ���q�w�ߥ[�H��������
�z�F�ǧQ�S�]Jellet�^�b1873�~�A�S�S���N�ҡ]Van�zt Hoff�^�b1877�~�S���s�o�{�F
�o�өw�ߡC�o�өw�ߤ����p�W�ҭz�A�i�Ѥ��l�B�ʲz�ױ��X�A�]�i�ھڼ��O�ǭ�z�q�H
�G��t����q���Y���ɥX�ӡC���b�\�h�ƾǤ������o�����W���ҩ��C
�W�����L�A���}���ϱۦb�������b���ɶi��o�ܧ֡A�_�h�i��o���C�C�����èS��
���ܤơA���n�H�u�P�i�����A�ۤv�ä��ѥ[�����C�o�@�{�H�b1812�~���������N�ҵo
�{�C�L�o�{�b�H���ķ��G���A�����i�ܤƬ�����}�C�����`�N��`��ϾJ�]�T�b�Ů�
��ơC�h����ǡ]Dobereiner�^��o�{�`�������i�ϲB��G��ƦX�C1838�~�A�w�Ԧ���
�]Cagniard de Latour�^�P�I���]Schwann�^�U���ۿѦa�o�{�}�ҥH��o�æӦ��s��P
�G��ƺҡA�O�ѩ�@�طL�ͪ����@�ΡA�f���d������X�o�ûP�`���ҫP�����L��������
�ۦ��ʡC�f���d����o�ا@�Υs���u�ʤơv�A���P���ƾǤ������վ��㦳�u�ʤƯ�O�v�C
�L���X�b�ͪ��餤�Ѵ��q����B�Ӫ��G�ĩΦ�ӥͦ����L�ƺؤƦX���A�i��O��������
�ƾ���������һs�����C1878�~�A�w���]Kuhne�^��o�Ǧ����ʤƾ��s���u���v�λï��C
1862�~�A���S���]Berthelot�^�P�t�N�Ǵ��]Pean de St Gilles�^�o�{�A�p�����l
��ұN�A��L�ĻP���V�X�A�g�L�X�P������A�A��L�ĴN�������ѦӦ��A�J�P�L�ġA��
�ƪ��t�O����C�p�G�q�s��P�Ķ}�l�A�h�ƾ��ܤƴ¤Ϥ�V�i��A�̫ᥭ�Ůɪ���
�ҬO�ۦP���C�o�Ǥ����ܺC�A���p���q�Ħb���A�h�X�I�����Y�i�F��P�˪����šC�o��
�ĴN���F�@�ضʤƾ��A�ӥB�i�H�ݥX�A�ʤƾ����\�Φb��P�i��Ӥ�V������@�Ӥ�V
���ƾǤ����C�q�Y�طN�q�W���A�����@�ΡA�n�H�Ƽ���������Ұ_���@�Τ@�ˡC1887�~�A
���֧Q�Q���]Arrhenius�^�o�{�������ʤƧ@�λP��ɹq�v�����C
����]���P�˪��{�H�C1880�~�A�f�J���]Dixon�^�o�{�p�G�B��G��ܰ���A�o��
�خ���N�����z���Ӧ�����C1794�~�A�I�ǩi�]Fulhame�^�ҤH�w���[���o�Ӳ{�H�C
1902�~�A���J�]BreretonBaker�^���X�A�p�ƦX�i��o�ܺC�åB�Φ��F���A�N�S���z��
�{�H�C���i���S�ԡ]Armstrong�^���ܡA�����ۨ��ҧΦ������L��º�A�S���ʤƧ@�ΡC
�ڧڭ̩Ҫ��A�٦��@�ǮɭԡA�º骺�ƾǪ���]�O���_�@�Ϊ��A���G�����������V�X��
�b���A�~��P�i�ܤơC�����ʤƾ��Ρ��b�ͪ���ǤW�����n�ʱN�b�H��X�����ԭz�C
�Q�E�@���̫�X�~�o�{�F�X�ӷs���k�ʤ����C1895�~�A�ĤT�N�p�Q��h�]third
Lord Rayleigh�^�`�N��A�q�Ů�o�Ӫ����q��ƦX���o�Ӫ��A�K�n�j�@�ǡA�]��
�ɤޥL�M�ԩi�ɵo�{�F�@�شk��A�R�W����C��۵o�{���٦���]�Ѭ�241���^�B�ߡB
���P�I�A�o�O�|�~���q�Ů�̵o�{�����ӷs�����C��{�b�Ω�K�����R��q�O�A��P��
�Ω�s�i�O�i�O�A���]������㦳��z�ʡA��Ω�O��C�M�O���ѵM��@�D�q�[���j�M
���ꪺ�Y�Ǥg�a�̳v�X�����A�L�h�ΨӥR��W����y�C�o�Ǥ����b���o�C�C�ҩP
�������Φ���l�����s���@�ڡA�Ӧb�H��n�ԭz�������Q����l�Ǽƪ��̤]����A����
�a��C�����y���H��ӹ���l�q�P�P����Ҷi�檺��s�ϱo�o�Ǯ���b�z�פW��H�e
��[���n�C
���G�z��
����b�����Ψ�L�G�餤�i�H���ѡA�o�O�H�Ҽ������{�H�C���DzG��A�p�s��P���A
�������ҳ��i���۲V�X�A�Ӧ��DzG��p�o�P���A�@�I�]����V�X�C�T��p�}�i�b����
�ۥѷ��ѡA���ݴN�����ѡF�Ů�P����������Ȥֳ\���ѩ���A�Ӯ��P�B��Į�h�j
�q���ѡC
���z�ܤƥi�P���ѦP�ɵo�͡C���G���e�n�i���M�����ۥ[���e�n�p�A�ӥB�i
��l���M����{�H�C�\�h�����Q���ѩ���ɲ��ͭP�N�����A�i�O�]���ּ��Q���p���
�T���Ѯɵo�X���ӡC�����P�P���]�`�o���C
�o�Ǥ����A�g�L�\�h�ƾǮa��s�C�L�̻{�Ѩ�o�ؤ������ʽ�ܽ����A�䤤���V�X
�P�ƦX��ر��ΡA���L�A���̪��������_���ܡ]�P��L�ƦX�������@�w��Ҥ��P�^����
�䶡�s�b���@�ǯS�����Y�C���b�Q�E�@���H�e�S���H�N���G�{�H���@�S�����D�C
�������t�Φa��s���Ѫ��誺�X�����H�O��p�̩i�]ThomasCraham�A1805��1869
�~�^�C�L�������X��������A�ڭ̦b�e���w�g���L�F�C��p�̩i�o�{�A����A�p�\�h
�Q���A���ѩ���ɡA�`��ۥѦa��L�����A�i�H����֦a�q���G���@�����X����t�@��
���C�������@�����Φ����骺����A���ѫ��X������w�C�C��p�̩i�ٲĤ@�����鬰��
����A�ĤG��������C�_��H�����饲�w�O�������A����Ӥ~���D�\�h�L�����p���Ư~�A
�Ʀܪ��ݦp�����A�g�L�S���B�z�A�]�i�H�e���骬�A�C
��S�q�����o���H�Υߨ��H���ӨӪ����G�q�ѩʽ誺��s�A�w�g�ԭz�L�F�C
1833�~�A�k�Բī��X�A�Ϥ@�w�q�q�q�L�q�ѲG�ɡA�`�O���@�w�q�����l�b�q���W�R�X�C
�p�G�ڭ̧�q�y�ݧ@�O�a���l���B�ʦӶǻ����A�o�N�N���ۨC�@�ӭ�l���ۦP�����l��
�w�a�ۦP�˪��q���A�o�˳�����l�ұa���q���A�N���F�۵M�����ιq��l�C
1859�~�A�Ʀ��ҡ]Hittorf�^�b�o�Ӱ��D�W�S�e�i�F�@�B�C�L���q�y�q�L��Ӥ���
���q���A���G��ӹq�������G�N�{�פ����a�}���_�ӡC�Ʀ��ҬݥX�A�Q�γo�Өƹ�
�N�i�H�ι����k�ⲧ�����l�B�ʪ��t�ץ[�H����A�]�o��t���j�����l���q������
�h���h���q�ѽ�C�o�˴N�i�H���w��ز������l���t�פ�C
1879�~�A�캸�ҬI�]Kohlrausch�^�o���A�@�Ӵ��q�q�ѲG�q�����n��k�C�ѩ�
�@�ΡA���y�q�O����ϥΪ��A���캸�ҬI�o�J�A�F�o�ӧx���C�L���ΤF��y�q�M�j���n
���������q���A�Ӵ�֨I�����������K�סC�L���ιq�y�p�A�ӥι��y�q���������q��
���ӧ@���ܾ��C�b�o���קK�F���Ƨ@�Τ���A�L�o�{�q�ѲG�]�A�q�کi�w�ߡA�Y�q�y�P
�q�ʤO����ҡC�]���̤p���q�ʤO�]�i�H�Ϲq�ѽ褤���ͬ������q�y�F���F�b�q������
���~�A�]�S�����ƪ��ϧ@�ΡC�ҥH���l���w�i�H�ۥѥ洫�A���J�ҭE���һ������ˡC
�캸�ҬI�N�o�˴��w�F�q�ѽ誺�Ǿɲv�A�åB���X�ѩ�q�y���ϦV���l�y�Ҷǰe�A
�Ǿɲv�@�w�i�H�ΨӴ��q�ϦV���l�t�ת��`�M�C�A�[�W�Ʀ��Ҫ����w���l�t�פ���
�k�A�ڭ̴N�i�H�p��ӧO���l���t�פF�C�b�C���̦�1��S�q��t����פU�A�B�b����
�B�ʪ��t���C��0�D003���̡A�Ӥ����Q�������l���t�h�����C��0�D0006���̡C�B
���l���t�ȡA�g���v�]Oliver Lodge�^��h�b���礤�[�H�ҹ�C�L�Τ@�ع�B�F�Ӫ�
���ܾ��������ۦ�A�ϲB���l�q�L�䤤�A�M��[�H�l��C�����Q���l���ƭȡA�h������
�@�̩��ҹ�]���ѧ@���[��F���̦b�ۦ��Q�������B�ʡ^�A�q�I�����Φ����]�i�H�o��
�ҹ�C�o�Ǥ�k�H��S�Ѱ��ˡ]Masson�^�B�������]Steele�^�B���������]Maclnnes�^
����s�̥[�H��i�C
�������z�Ǯa�S�S-�N�ҹ�G���t�~�@�جݪk�C�ڭ̦��w���D�A�g�L�ӭM����
���J�Ӫ��ӭM�����A�i�H���ͤ@�����O�A�Ӫ��Ǯa�إ��]Pfeffer�^�ΤH�u�����A�Y�b
�L�V�����W�ΤƾǤ�k�y���I���ӻs���������A�q�L�o�غ��z���C�S�S-�N�ҫ��X�A
�إ������q�����A���z���M��L�]�������Y�ܶH���骺���O�A�Y�P�e�n���Ϥ�A���H��
��ūצӼW�[�C�b���G���ຯ�z���������A���Ψ�L�����i�H�i��i�f�����z���{�H��
�ڭ̥i�H�]�Q�㦳���z�ʪ��ӭM�N�O�@�Ӳz�Q�������T���A�]���A�S�S-�N�ҥi�H���
�O�Ǫ����z���Ψ췻�G�W�h�A�q�Ӷ}�P�F�@�ӷs����s���C�L�N���G�����z���M��L
���z�ʽ�p���T�I�B�T�����pô�_�ӡA�o�ˡA�q�L���q���T�I�]�o�O�@������e������
�u�@�^�A�N�i�H��X���z���C�L�q�z�פW�ҩ��}���G�����z��������ȥ��P�P�@�ת���
�����O�ۦP�A�M��L�S�ι����ҩ��F�o�ӵ��G�C�ڭ̨ä�����ǤH�ҳ]�Q�����˦]��
�N�o�X�����F������O�㦳�ۦP����]�A�η��Ѫ�����O���ۮ��骬�A�C���O�Ǫ���
�z�ä��A�ξ�����D�A���������pô���q���������Y�A���o���A�γo���pô���ʽ�C
���z���]�\�H���骺���O�@�ˡA�O�ѩ���l���I���Ӳ��ͪ��F�]�\�O�ѩ�P������
�����ƾǿ˦X�O�ΤƾǤƦX�Ӳ��ͪ��C���ޥ����ʽ��ˡA�u�n���s�b�A���N���w�A�X
���O�ǭ�z�A�b�}���G���A�p�S�S���N�ҩ��ҩ����A���N���w���`����w�ߡC�i�O����
��]���w�A�ܤ֤��O���O�ǩү�T�w���C
1887�~�A���H���֧Q�Q���ҩ����z���P���G���q�ѩʦ����D�ڭ̳����D�A�q�ѽ�
�����z�����`���j�A�Ҧp��ƹ[�Υ����������G���Q�������G�A�����O���P���l�@�ת�
�}���G�����O���⭿�C���֧Q�Q���o�{�A�o�دS�j�����O�����P�q�Ѫ��ɹq�צ����A��
�B�P�ƾǪ����ʩʡA�p�����b�}�o�æ��ܬ��s�몺�L�{�����ʤƯ�O�]�����Y�C�L����
�O�o�����O�����q�ѽ褤���l�������ѡA�]���A�|�Ҩӻ��A�b��ƹ[���G���A���M��
�Y�z���ʪ�KCI���l�s�b�A�P�ɤ]���[���l�P�����l�U�a�ۥ��q���P�t�q���A�������G
�ɹq�P�ƾǬ��ʩʪ��ӷ��C���G�V�H�A���Ѫ��Q�V�h�A�췻�G�H�췥�ɡA�G���u��
K�����l�MCI�����l�C���H�{���o������l�������}�A�O�M�����ƦX�b�@�_���C
�캸�ҬI�B�S�S���N�ҡB���֧Q�Q�����u�@���F���z�ƾǪ��e�j���W�h�j�H���_�I�C
�b�o�y�j�H�̡A���O�ǻP�q�ǵ��X�_�ӡA�ϲz�ת����Ѥ��_�a�W�i�A�åB�U�ӷU�s�x�a
������Ω�u�~�C�����p���A�ڭ̤]���n�ѰO��Ӧ��@�ǰ��j�����z�Ǯa��s�F�q�b��
�餤���ǾɡA�ئ��F�{�N��Ǥ��̦��S�x�ʪ��@�Ӥ���A�ӥL�̪����l�[���o�O���G�z
�����L�̪��C
�q���窺�[�I�ӬݡA�������w���z���O�ܧx�����A���O�A���ꪺ�������]Morse�^
�P�h�S���]Whitney�^�A�H�έ^�ꪺ���J�ܡ]Berke��ley�^�B��P���S�ܡ]E�DG�DJ�D
Hartley�^�A�o����b1901�~�M1906��1916�~���A�ﰪ�@�ת����G�������z���i��F��
�����w�C�������P�L���P�ƩҥΪ����w��k�W�P�إ�����k�ۦP�A�u�O�b�Ӹ`�W�j
����i�C���J�ܻP���S�ܨèS���[������y�J�b�b���z���p�Ǹ̳y�������O�A�ӬO��
���G����v���W�������O�A���췻������B�ʪ���V�Q�����X�h�C�L�̧�ұo�����G�M
�S�E�w�E�˺�����{���]��232���^�[�H����F�N���}�P����}�Ө��A�o�{�P�U�C����
�̲ŦX�G
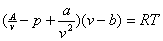 �����S�˺��w�]ostwald�^���q�@�Ϊ��ƾǩw�ߡ]245���^���Ω���֧Q�Q���ҷQ
�H���q�ѽ誺���ѡA���@�ӵ}�Ʃw�ߡG
�����S�˺��w�]ostwald�^���q�@�Ϊ��ƾǩw�ߡ]245���^���Ω���֧Q�Q���ҷQ
�H���q�ѽ誺���ѡA���@�ӵ}�Ʃw�ߡG
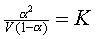 �����\�N���q���סAV�N�����G���e�n�AK�O�`�ơC�o�Ӥ�{�����z���q�ѽ観�ġA
�p�������Ѫ��ĩM�Q�A�o�ɤW���ܬ�
�����\�N���q���סAV�N�����G���e�n�AK�O�`�ơC�o�Ӥ�{�����z���q�ѽ観�ġA
�p�������Ѫ��ĩM�Q�A�o�ɤW���ܬ�
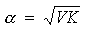 ������������Ѫ��q�ѽ�L�ġA�o�@���ѡA���ܪ��ɶ������q���z�פ��ର�H
�������@�ӻ�ê�C
�o�ӧx�����̪�s�j��W�J�A�C1923��1927�~���A�w���]Debxe�^�B�溸
�]Huckel�^�P���Į�]onsager�^���X�A�ѩ����l�����@�ΤO�A���l�P��Φ��@�ز���
�����l�j��C���l�B�ʮɡA�����b�e���ذ_�@�ӷs���j��A�Ө�I�᪺�j������C�o�@
�@�ΧΦ��@�ت��ת��q�즲�A�ϥ����B�ʡA�P��@�ת�����ڦ���ҦӴ�֡C�o�˴N��
�X�@�Ӭ۷���������{���C�p�N���l���i��l�X�@�֭p�J�A�o�Ӥ�{���P����ӱo��
���Y�A�Y�@�P�ɹq�ת����Y�A�j�P�ŦX�A�N�O��j�q�ѽ�@���G�ӻ��]�O�p���C
���֧Q�Q�{���j�q�ѽ�u���������ѡA�ӳ̪�s�o�����O�����q���C�ܩ�@��
�G�̬۹�q���ת���֡A���O�ѩ����l�t�ת��ܽw���t�G�C��X�g�u���R�A������l�N
�O�b�T�A�����餺�A�]�O�������}�A�H��A�]���H���X�o�˪��ݪk�]��384�A427��8��
���^�C
------------------
�@�@
������������Ѫ��q�ѽ�L�ġA�o�@���ѡA���ܪ��ɶ������q���z�פ��ର�H
�������@�ӻ�ê�C
�o�ӧx�����̪�s�j��W�J�A�C1923��1927�~���A�w���]Debxe�^�B�溸
�]Huckel�^�P���Į�]onsager�^���X�A�ѩ����l�����@�ΤO�A���l�P��Φ��@�ز���
�����l�j��C���l�B�ʮɡA�����b�e���ذ_�@�ӷs���j��A�Ө�I�᪺�j������C�o�@
�@�ΧΦ��@�ت��ת��q�즲�A�ϥ����B�ʡA�P��@�ת�����ڦ���ҦӴ�֡C�o�˴N��
�X�@�Ӭ۷���������{���C�p�N���l���i��l�X�@�֭p�J�A�o�Ӥ�{���P����ӱo��
���Y�A�Y�@�P�ɹq�ת����Y�A�j�P�ŦX�A�N�O��j�q�ѽ�@���G�ӻ��]�O�p���C
���֧Q�Q�{���j�q�ѽ�u���������ѡA�ӳ̪�s�o�����O�����q���C�ܩ�@��
�G�̬۹�q���ת���֡A���O�ѩ����l�t�ת��ܽw���t�G�C��X�g�u���R�A������l�N
�O�b�T�A�����餺�A�]�O�������}�A�H��A�]���H���X�o�˪��ݪk�]��384�A427��8��
���^�C
------------------
�@�@